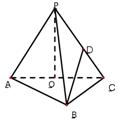
题目内容
在三棱锥P-ABC中,△ABC是正三角形,∠PCA= ,D为PA中点,二面角P-AC-B为
,D为PA中点,二面角P-AC-B为 ,PC=2,AB=
,PC=2,AB= .
.
(1)求证AC⊥BD;
(2)求BD与底面ABC所成的角(用反正弦表示);
(3)求三棱锥P-ABC的体积.
答案:
解析:
解析:
|
解 (1)如图,取AC中点E,连结BE,DE,则DE∥PC.由PC⊥AC,知DE⊥AC.由△ABC为正三角形,得BE⊥AC.又DE∩BE=E,所以AC⊥平面DEB,
(2)由AC⊥平面DEB, 由DE⊥AC,BE⊥AC,知∠DEB是二面角P-AC-B的平面角.在△DEB中,DE=1, 由正弦定理,得 ∴sin∠DBE= ∴所求角为arc sin 另一解法是由AC⊥平面DEB, 作DF⊥平面ABC,F是垂足,F在BE的延长线上,∠DBF是DB与平面ABC所成的角. 由DE⊥AC,BE⊥AC,知∠DEB是二面角P-AC-B的平面角. 在 Rt△DBF中,DE= 由余弦定理,知BD= (3)∵AC⊥平面DEB, ∴平面DEB⊥平面PAC. 作B到平面PAC的垂线BG,G为垂足,G在DE的延长线上. 在Rt△BEG中,∠BEG=
或由DF= ∴ |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .于是AC⊥DB.
.于是AC⊥DB.
 ,知平面DEB⊥底面ABC,∠DBE是DB与底面ABC所成角.
,知平面DEB⊥底面ABC,∠DBE是DB与底面ABC所成角. ,∠DEB=
,∠DEB= .故得
.故得 -2×1×3×cos
-2×1×3×cos .
. ,
, .
. ,知平面DEB⊥平面ABC.
,知平面DEB⊥平面ABC. PC=1,BE=
PC=1,BE= AB=3,∠DEB=
AB=3,∠DEB= ,DF=
,DF= .
. ,sin∠DEF=
,sin∠DEF= =
= ,故可得DB与底面ABC所成角为arc sin
,故可得DB与底面ABC所成角为arc sin ,
, .
. .
. ,知P到平面ABC的距离为2DF=
,知P到平面ABC的距离为2DF= .
. .
.