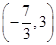题目内容
若关于x的不等式|2x-1|-|x-3|<m在x∈[0,4]上有解,则m的取值范围为 .
分析:不等式|2x-1|-|x-3|<m在x∈[0,4]上有解,等价于f(x)min<m,令f(x)=|2x-1|-|x-3|,按照0≤x≤
,
<x≤3,3<x≤4三种情况进行讨论,可求得x∈[0,4]时,f(x)min=-
,从而可得答案.
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
解答:解:令f(x)=|2x-1|-|x-3|,
①当0≤x≤
时,f(x)=-(2x-1)+(x-3)=-x-2,
此时,-
≤f(x)≤-2;
②当
<x≤3时,f(x)=(2x-1)+(x-3)=3x-4,
此时,-
<f(x)≤5;
③当3<x≤4时,f(x)=(2x-1)-(x-3)=x+2,
此时,5<f(x)≤6;
综上,x∈[0,4]时,f(x)min=-
,
又不等式|2x-1|-|x-3|<m在x∈[0,4]上有解,等价于f(x)min<m,
∴m>-
,即m的取值范围为:(-
,+∞),
故答案为:(-
,+∞).
①当0≤x≤
| 1 |
| 2 |
此时,-
| 5 |
| 2 |
②当
| 1 |
| 2 |
此时,-
| 5 |
| 2 |
③当3<x≤4时,f(x)=(2x-1)-(x-3)=x+2,
此时,5<f(x)≤6;
综上,x∈[0,4]时,f(x)min=-
| 5 |
| 2 |
又不等式|2x-1|-|x-3|<m在x∈[0,4]上有解,等价于f(x)min<m,
∴m>-
| 5 |
| 2 |
| 5 |
| 2 |
故答案为:(-
| 5 |
| 2 |
点评:本题考查函数恒成立问题,考查转化思想、分类讨论思想,考查学生分析解决问题的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若关于x的不等式2-x2>|x-a|至少有一个负数解,则a的取值范围为( )
A、(-
| ||
B、(-
| ||
C、(-
| ||
D、(-
|
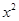 >|x-a|
至少有一个负数解,则实数a的取值范围是
.
>|x-a|
至少有一个负数解,则实数a的取值范围是
.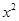 >|x-a| 至少有一个负数解,则a的取值范围为(
)
>|x-a| 至少有一个负数解,则a的取值范围为(
)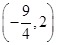 B.
B.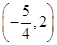 C.
C.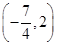 D.
D.