题目内容

如图,平面α∥平面β,线段AB交α、β于M、N,线段AD分别交α、β于C、D,线段BF分别交α、β于F、E,若AM=9,MN=11,NB=15,S△FMC=78,求△END的面积.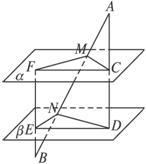

解:∵AB∩AD=A,

    ∴AB、AD确定平面ABD.

    而MC、ND为平面ABD与平面α、β的交线,

    ∴MC∥ND.同理可得FM∥EN.

    于是∠FMC=∠END.

    ∴==·=·=.

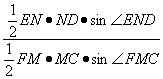    ∴S△END=S△FMC=×78=100.

讲评:在运用两平面平行的性质定理时,一定要先找到与两平行平面都相交的第三个平面,继而推得两交线平行.

练习册系列答案
相关题目
（理科）如图的多面体是底面为平行四边形的直四棱柱ABCD-A1B1C1D1，经平面AEFG所截后得到的图形．其中∠BAE=∠GAD=45°，AB=2AD=2，∠BAD=60°．
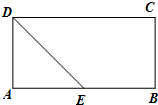
精英家教网
（Ⅰ）求证：BD⊥平面ADG；
（Ⅱ）求平面AEFG与平面ABCD所成锐二面角的余弦值．

（文科）如图，AB为圆O的直径，点E、F在圆O上，AB∥EF，矩形ABCD所在的平面和圆O所在的平面互相垂直，且AB=2，AD=EF=1．
（Ⅰ）求证：AF⊥平面CBF；
（Ⅱ）设FC的中点为M，求证：OM∥平面DAF．
精英家教网
精英家教网精英家教网如图，在矩形ABC中，AB=4，AD=，E为AB的中点，现将△ADE沿直线DE翻折成△A′DE，使A′在平面BCDE的射影在DE上，F为线段A′D的中点．
（Ⅰ）求证：EF∥平面A′BC；
（Ⅱ）求直线A'C与平面A′DE所成角的正切值．
如图（1）直线l∥AB，且与CA，CB分别相交于点E，F，EF与AB间的距离是d，点P是线段EF上任意一点，Q是线段AB上任意一点，则|PQ|的最小值等于d．类比上述结论我们可以得到：在图（2）中，平面α∥平面ABC，且与DA，DB，DC分别相交于点E，F，G，平面α与平面ABC间的距离是m，
a，b分别是平面α与平面ABC内的任意一条直线，则a，b间距离的最小值是m．
或P，Q分别是平面α与平面ABC内的任意一点，则P，Q间距离的最小值是m．
a，b分别是平面α与平面ABC内的任意一条直线，则a，b间距离的最小值是m．
或P，Q分别是平面α与平面ABC内的任意一点，则P，Q间距离的最小值是m．
．
如图，平面ABDE⊥平面ABC，△ABC是等腰直角三角形，AC=BC=4，四边形ABDE是直角梯形，BD∥AE，BD⊥BA，BD=
12
AE=2，O、M分别为CE、AB的中点．
（1）求异面直线AB与CE所成角的大小．
（2）求直线CD和平面ODM所成角的正弦值．
如图，平面α⊥平面β，α∩β=l，DA?α，BC?α，且DA⊥l于A，BC⊥l于B，AD=4，BC=8，AB=6，点P是平面β内不在l上的一动点，记PD与平面β所成角为θ1，PC与平面β所成角为θ2．若θ1=θ2，则△PAB的面积的最大值是
12
12
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网