Question

 在ΔABC中，AB=AC，∠A=900，过A引中线BD的垂线与BC交于点E，求证：∠ADB=∠CDE。

Answer 1

 见图10-1，以A为原点，AC所在直线为x轴，建立直角坐标系。设点B，C坐标分别为（0,2a）,(2a,0)，则点D坐标为（a, 0）。直线BD方程为，  ①直线BC方程为x+y=2a，   ②设直线BD和AE的斜率分别为k1, k2，则k1=-2。因为BDAE，所以k1k2=-1.所以，所以直线AE方程为，由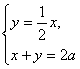解得点E坐标为。

所以直线DE斜率为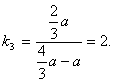因为k1+k3=0.

所以∠BDC+∠EDC=1800，即∠BDA=∠EDC。