题目内容
设α为三角形的一个内角，且
，则cos2α=
- A.
- B.
- C.或
- D.
A
分析：把已知的等式左右两边平方，再利用同角三角函数间的基本关系及二倍角的正弦函数公式化简，求出sin2α的值，再求出cosα-sinα，即可求出cos2α的值．
解答：∵，∴两边平方可得sin2α=-
∵α为三角形的一个内角，∴sinα＞0，cosα＜0
∴cosα-sinα=-
=-
∴cos2α=（cosα+sinα）（cosα-sinα）=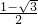
×（-）=
故选A．
点评：本题考查了同角三角函数间的基本关系，二倍角的正弦公式，考查学生的计算能力，属于基础题．
分析：把已知的等式左右两边平方，再利用同角三角函数间的基本关系及二倍角的正弦函数公式化简，求出sin2α的值，再求出cosα-sinα，即可求出cos2α的值．
解答：∵
，∴两边平方可得sin2α=-∵α为三角形的一个内角，∴sinα＞0，cosα＜0
∴cosα-sinα=-
=-∴cos2α=（cosα+sinα）（cosα-sinα）=
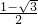×（-）=故选A．
点评：本题考查了同角三角函数间的基本关系，二倍角的正弦公式，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
a2＝
(r1＋r2＋r3)a，可得正三角形内任一点到三边的距离之和是一个定值，即r1＋r2＋r3＝
a．类比到棱长为a的正四面体内一点P，它到正四面体各面的距离之和是定值________．
a2＝
(r1＋r2＋r3)a，可得正三角形内任一点到三边的距离之和是一个定值，即r1＋r2＋r3＝
a．类比到棱长为a的正四面体内一点P，它到正四面体各面的距离之和是定值________．
为平面
内的
个点。在平面
到点
上的任意点都是端点
的中位点。现有下列命题：
共线，
在线段
共线，则它们的中位点存在且唯一；