题目内容
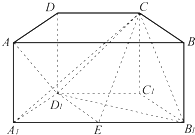 如图,在直四棱柱ABCD-A1B1C1D1中,底面A1B1C1D1是梯形,且A1B1∥D1C1,A1D1=D1D=D1C1=
如图,在直四棱柱ABCD-A1B1C1D1中,底面A1B1C1D1是梯形,且A1B1∥D1C1,A1D1=D1D=D1C1=| 1 | 2 |
(1)求证:CD⊥AD;
(2)求点C1到平面CD1B1的距离;
(3)求二面角D1-CE-B1的大小.
分析:(1)连结A1D,由正方形的性质得AD1⊥DA1,结合AD1⊥A1C证出AD1⊥平面A1CD,从而AD1⊥CD.再由直棱柱的性质得DD1⊥CD,利用线面垂直的判定定理得CD⊥平面AA1D1D,从而证出CD⊥AD;
(2)算出△CD1B1中各边长,从而得到△CD1B1为直角三角形,得到△CD1B1的面积,根据三棱锥C-C1D1B1的体积等于三棱锥C1-CD1B1的体积,建立等式即可解出点C1到平面CD1B1的距离为h.
(3)取CE的中点F,连结D1F,由(2)的结论得△D1CE是正三角形,可得D1F⊥CE,结合CE∥A1D得A1B1⊥CE.取CB1的中点G,连结FG则CE⊥FG,得∠D1FG是二面角D1-CE-B1的平面角.然后在△D1FG中,根据D1F、FG的长,算出D1G长.最后在△D1FG中,由余弦定理算出cos∠D1FG=-
,即可得到二面角D1-CE-B1的大小.
(2)算出△CD1B1中各边长,从而得到△CD1B1为直角三角形,得到△CD1B1的面积,根据三棱锥C-C1D1B1的体积等于三棱锥C1-CD1B1的体积,建立等式即可解出点C1到平面CD1B1的距离为h.
(3)取CE的中点F,连结D1F,由(2)的结论得△D1CE是正三角形,可得D1F⊥CE,结合CE∥A1D得A1B1⊥CE.取CB1的中点G,连结FG则CE⊥FG,得∠D1FG是二面角D1-CE-B1的平面角.然后在△D1FG中,根据D1F、FG的长,算出D1G长.最后在△D1FG中,由余弦定理算出cos∠D1FG=-
| ||
| 3 |
解答:解:(1)连结A1D,
∵四边形A1D1DA是正方形,∴AD1⊥DA1,
又∵AD1⊥A1C,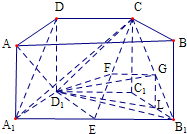 DA1、A1C是平面A1CD内的相交直线,
DA1、A1C是平面A1CD内的相交直线,
∴AD1⊥平面A1CD,
∵CD?平面A1CD,∴AD1⊥CD,
又∵DD1⊥CD,DD1、AD1是平面AA1D1D内的相交直线,
∴CD⊥平面AA1D1D,
∵AD?平面AA1D1D,∴CD⊥AD…(5分)
(2)用等体积法:
设点C1到平面CD1B1的距离为h,
在△CD1B1中,CD1=
,D1B1=
,CB1=
,
∴△CD1B1为直角三角形,
由VC-C1D1B1=VC1-CD1B1,得
×1×
×1×
sin135°=
×
×
×
×h,
解之得h=
,
∴点C1到平面CD1B1的距离为
.
(3)由(2)得D1E=D1C=CE=A1D=
,
取线段CE的中点F,连结D1F,则D1F⊥CE,
∵CE∥A1D,∴A1B1⊥CE,
再取线段CB1的中点G,连结FG
∴FG∥EB1,可得CE⊥FG,得∠D1FG是二面角D1-CE-B1的平面角,
在△D1FG中,D1F=
,FG=
,取线段B1C1的中点L,连结GL,
则D1G2=GL2+D1L2,
在△D1C1L中,D1L2=1+
-2•1•
cos135°=
,
∴D1G2=
+
=
,
△D1FG中,由余弦定理,得cos∠D1FG=
=-
,
∴二面角D1-CE-B1的大小为arccos(-
).…(14分)
∵四边形A1D1DA是正方形,∴AD1⊥DA1,
又∵AD1⊥A1C,
 DA1、A1C是平面A1CD内的相交直线,
DA1、A1C是平面A1CD内的相交直线,∴AD1⊥平面A1CD,
∵CD?平面A1CD,∴AD1⊥CD,
又∵DD1⊥CD,DD1、AD1是平面AA1D1D内的相交直线,
∴CD⊥平面AA1D1D,
∵AD?平面AA1D1D,∴CD⊥AD…(5分)
(2)用等体积法:
设点C1到平面CD1B1的距离为h,
在△CD1B1中,CD1=
| 2 |
| 5 |
| 3 |
∴△CD1B1为直角三角形,
由VC-C1D1B1=VC1-CD1B1,得
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
解之得h=
| ||
| 6 |
∴点C1到平面CD1B1的距离为
| ||
| 6 |
(3)由(2)得D1E=D1C=CE=A1D=
| 2 |
取线段CE的中点F,连结D1F,则D1F⊥CE,
∵CE∥A1D,∴A1B1⊥CE,
再取线段CB1的中点G,连结FG
∴FG∥EB1,可得CE⊥FG,得∠D1FG是二面角D1-CE-B1的平面角,
在△D1FG中,D1F=
| ||
| 2 |
| 1 |
| 2 |
则D1G2=GL2+D1L2,
在△D1C1L中,D1L2=1+
| 1 |
| 2 |
| ||
| 2 |
| 5 |
| 2 |
∴D1G2=
| 5 |
| 2 |
| 1 |
| 4 |
| 11 |
| 4 |
△D1FG中,由余弦定理,得cos∠D1FG=
(
| ||||||||
2•
|
| ||
| 3 |
∴二面角D1-CE-B1的大小为arccos(-
| ||
| 3 |
点评:本题在直四棱柱中证明线面垂直,求二面角的大小并求点到平面的距离.着重考查了直四棱柱的性质、线面垂直的判定与性质、等体积法求点面距离和二面角的平面角的定义与求法等知识,属于中档题.

练习册系列答案
相关题目
 18、如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点,F为AB的中点.证明:
18、如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点,F为AB的中点.证明: 18、如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点.
18、如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点. 15、如图,在直四棱柱ABCD-A1B1C1D1中,A1C1⊥B1D1,E,F分别是AB,BC的中点.
15、如图,在直四棱柱ABCD-A1B1C1D1中,A1C1⊥B1D1,E,F分别是AB,BC的中点. 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1,F分别是棱AD,AA1,AB的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1,F分别是棱AD,AA1,AB的中点. (2010•抚州模拟)如图,在直四棱柱ABCD-A1B1C1D1中,AB=BC,∠ABC=60°,BB1=BC=2,M为BC中点,点N在CC1上.
(2010•抚州模拟)如图,在直四棱柱ABCD-A1B1C1D1中,AB=BC,∠ABC=60°,BB1=BC=2,M为BC中点,点N在CC1上.