题目内容
设集合U={1,2,3,4,5},A={1,2},B⊆U,则满足A∩B={1,2}的集合B有
- A.1个
- B.3个
- C.4个
- D.8 个
D
分析:由A∩B={1,2}=A,说明集合A是集合B的子集,又B⊆U,根据子集概念可分析组成集合B的元素情况,从而得到集合B的个数.
解答:由A∩B={1,2}=A,则A⊆B,
由集合U={1,2,3,4,5},B⊆U,
所以集合B中的元素一定含有1,2,
然后在从3,4,5三个元素中一个不取,或任取一个,任取两个,或全取出构成集合B.
所以组成的集合B的个数为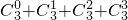 =23=8(个).
=23=8(个).
故选D.
点评:本题考查了交集及其运算,考查了子集的概念,若集合A含有n个元素,则其子集个数为2n个,是基础题.
分析:由A∩B={1,2}=A,说明集合A是集合B的子集,又B⊆U,根据子集概念可分析组成集合B的元素情况,从而得到集合B的个数.
解答:由A∩B={1,2}=A,则A⊆B,
由集合U={1,2,3,4,5},B⊆U,
所以集合B中的元素一定含有1,2,
然后在从3,4,5三个元素中一个不取,或任取一个,任取两个,或全取出构成集合B.
所以组成的集合B的个数为
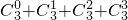 =23=8(个).
=23=8(个).故选D.
点评:本题考查了交集及其运算,考查了子集的概念,若集合A含有n个元素,则其子集个数为2n个,是基础题.

练习册系列答案
相关题目