题目内容
已知函数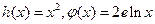 (其中e为自然对数)
(其中e为自然对数)
(1) 求F(x)=h(x)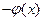 的极值。
的极值。
(2) 设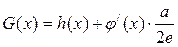 (常数a>0),当x>1时,求函数G(x)的单调区
(常数a>0),当x>1时,求函数G(x)的单调区
间,并在极值存在处求极值。
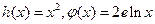 (其中e为自然对数)
(其中e为自然对数)(1) 求F(x)=h(x)
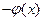 的极值。
的极值。(2) 设
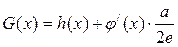 (常数a>0),当x>1时,求函数G(x)的单调区
(常数a>0),当x>1时,求函数G(x)的单调区间,并在极值存在处求极值。
(1)见解析;(2) 处有极小值,极小值为
处有极小值,极小值为
 处有极小值,极小值为
处有极小值,极小值为
解:(1) (x>0),
(x>0),

当0<x< 时,
时,  <0, 此时F(x)递减,
<0, 此时F(x)递减,
当x> 时,
时,  >0,此时F(x)递增
>0,此时F(x)递增
当x= 时,F(x)取极小值为0
时,F(x)取极小值为0
(2)可得 =
= ,
, ,
,
当x< 时,G(x)递减,当x>
时,G(x)递减,当x> 时,G(x)递增
时,G(x)递增
 x>1,
x>1,  若
若
 1时,即a
1时,即a 2,G(x)在(1,
2,G(x)在(1, )递增.,无极值。
)递增.,无极值。
若 >1时,即a>2,G(x)在(1,
>1时,即a>2,G(x)在(1, )递减,在(
)递减,在( ,
, ))递增。
))递增。
所以 处有极小值,极小值为
处有极小值,极小值为
 (x>0),
(x>0),
当0<x<
 时,
时,  <0, 此时F(x)递减,
<0, 此时F(x)递减, 当x>
 时,
时,  >0,此时F(x)递增
>0,此时F(x)递增 当x=
 时,F(x)取极小值为0
时,F(x)取极小值为0 (2)可得
 =
= ,
, ,
, 当x<
 时,G(x)递减,当x>
时,G(x)递减,当x> 时,G(x)递增
时,G(x)递增  x>1,
x>1,  若
若
 1时,即a
1时,即a 2,G(x)在(1,
2,G(x)在(1, )递增.,无极值。
)递增.,无极值。若
 >1时,即a>2,G(x)在(1,
>1时,即a>2,G(x)在(1, )递减,在(
)递减,在( ,
, ))递增。
))递增。所以
 处有极小值,极小值为
处有极小值,极小值为

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
 (其中e为自然对数的底数)
(其中e为自然对数的底数)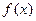 的奇偶性;
的奇偶性;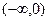 上求函数
上求函数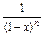 +aln(x-1),其中n∈N*,a为常数.
+aln(x-1),其中n∈N*,a为常数.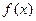 =
=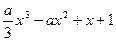 .
.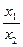 ≤5,求a的取值范围。12分
≤5,求a的取值范围。12分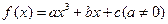 为奇函数,导函数
为奇函数,导函数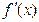 的最小值为-12,函数
的最小值为-12,函数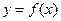 的图象在点P
的图象在点P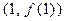 处的切线与直线
处的切线与直线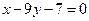 垂直.(1)求a,b,c的值;(2)求
垂直.(1)求a,b,c的值;(2)求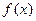 的各个单调区间,并求
的各个单调区间,并求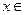 [-1, 3]时的最大值和最小值.
[-1, 3]时的最大值和最小值. 的最大值是( )
的最大值是( )



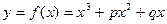 的图象与
的图象与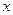 轴切于非原点的一点,且
轴切于非原点的一点,且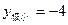 ,那么
,那么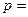 ,
,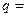
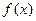 的定义域为区间
的定义域为区间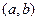 ,导函数
,导函数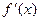 在
在
 个
个 个
个 个
个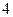 个[
个[