题目内容
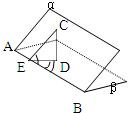已知二面角α-AB-β的平面角是锐角，C是平面α内一点（它不在棱AB上），点D是点C在面β上的射影，点E是棱AB上满足∠CEB为锐角的任一点，那么（ ）| A、∠CEB＞∠DEB | B、∠CEB=∠DEB | C、∠CEB＜∠DEB | D、∠CEB与∠DEB的大小关系不能确定 |
分析：作出图形，利用三垂线定理和直角三角形，推出∠CEB、∠DEB的正切值的大小，推出结论．
解答：
解：过C向AB做垂线交AB于F，连接DF，因为CD⊥AB又CF⊥AB，
所以AB⊥面CDF，所以CF垂直于AB
在直角三角形CDF中，CF为斜边DF为直角边，所以CF＞DF
易知tan∠CEF=
tan∠DEB=
由CF＞DF知，∠CEB＞∠DEB
故选A．
解：过C向AB做垂线交AB于F，连接DF，因为CD⊥AB又CF⊥AB，所以AB⊥面CDF，所以CF垂直于AB
在直角三角形CDF中，CF为斜边DF为直角边，所以CF＞DF
易知tan∠CEF=
| CF |
| FE |
| DF |
| FE |
由CF＞DF知，∠CEB＞∠DEB
故选A．
点评：本题考查三垂线定理，考查学生逻辑思维能力，是基础题．
练习册系列答案
相关题目
已知二面角α-AB-β的平面角是锐角θ，α内一点C到β的距离为3，点C到棱AB的距离为4，那么tanθ的值等于（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，已知二面角α-AB-β的大小为120°，PC⊥α于C，PD⊥β于D，且PC=2，PD=3．