题目内容
已知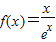 (e是自然对数的底数),
(e是自然对数的底数),(Ⅰ)求f(x)的单调区间;
(Ⅱ)设an=f(n),求数列{an}的前n项和Sn,并证明
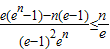 .
.
【答案】分析:(Ⅰ)求导函数,利用导数的正负,即可求f(x)的单调区间;
(Ⅱ)求出数列的通项.利用等比数列的求和公式求和,即可得到结论.
解答:解:(Ⅰ)∵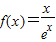 ,∴
,∴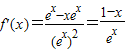 ,
,
当x<1时,f′(x)>0,f(x)是单调递增,当x>1时,f′(x)>0,f(x)是单调递减.
所以f(x)的递增区间是(-∞,1],递减区间是[1,+∞). …5分
(Ⅱ)∵an=f(n),Sn=a1+a2+…+an,∴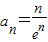 且
且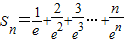 ,
,
∴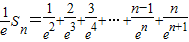
∴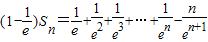 =
=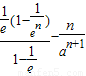
∴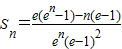 .
.
由(Ⅰ)知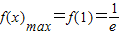 ,∴
,∴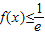 ,∴
,∴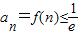 ,∴
,∴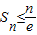 ,
,
∴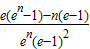
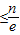 .…13分.
.…13分.
点评:本题考查导数知识的运用,考查导数的几何意义,考查不等式的证明,考查学生分析解决问题的能力,属于中档题.
(Ⅱ)求出数列的通项.利用等比数列的求和公式求和,即可得到结论.
解答:解:(Ⅰ)∵
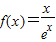 ,∴
,∴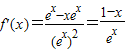 ,
,当x<1时,f′(x)>0,f(x)是单调递增,当x>1时,f′(x)>0,f(x)是单调递减.
所以f(x)的递增区间是(-∞,1],递减区间是[1,+∞). …5分
(Ⅱ)∵an=f(n),Sn=a1+a2+…+an,∴
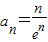 且
且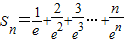 ,
,∴
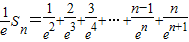
∴
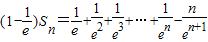 =
=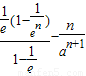
∴
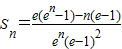 .
.由(Ⅰ)知
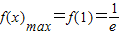 ,∴
,∴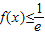 ,∴
,∴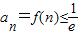 ,∴
,∴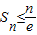 ,
,∴
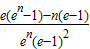
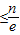 .…13分.
.…13分.点评:本题考查导数知识的运用,考查导数的几何意义,考查不等式的证明,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 其中e是自然对数的底数,
其中e是自然对数的底数,
 的单调性、极值;
的单调性、极值; 。
。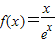 (e是自然对数的底数),
(e是自然对数的底数),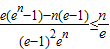 .
.