Question

如图，是一种加热水和食物的太阳灶，上面装有可旋转的抛物面形的反光镜，镜的轴截面是抛物线的一部分，盛水和食物的容器放在抛物线的焦点处，容器由若干根等长的铁筋焊接在一起的架子支撑.已知镜口圆的直径为12 m，镜深2 m.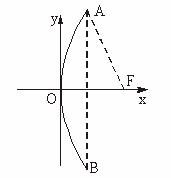

(1)建立适当的坐标系，求抛物线的方程和焦点的位置；

(2)若把盛水和食物的容器近似地看作点，试求每根铁筋的长度.

Answer 1

解:(1)如图，在反光镜的轴截面内建立直角坐标系，使反光镜的顶点(即抛物线的顶点)与原点重合，x轴垂直于镜口直径.

由已知，得A点坐标是(2，6).

设抛物线方程为y²=2px(p＞0),

则36=2p×2,p=9.

∴所求抛物线的标准方程是y²=18x,

焦点坐标是F(，0).

(2)∵盛水的容器在焦点处，∴A、F两点间的距离即为每根铁筋长.

|AF|= (或|AF|=+2=).

故每根铁筋的长度是6.5 m.