题目内容
求证:一圆的两条平行切线的切点连线经过圆心.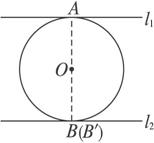
图
答案:已知:如图l1、l2分别切⊙O于A、B,l1∥l2,求证:O在AB上.
证明:连结OA,并延长交l2于B′,
∵l1切⊙O于点A,∴OA⊥l1.又∵l1∥l2,
∴OA⊥l2,即OB′⊥l2.
∴B为l2与⊙O的切点.∴OB⊥l2.
但过O只有一条直线与l2垂直.∴B′与B重合.
即A、O、B在一条直线上,或AB经过点O.
练习册系列答案
名校课堂系列答案
相关题目
名校课堂系列答案题目内容
求证:一圆的两条平行切线的切点连线经过圆心.
图
答案:已知:如图l1、l2分别切⊙O于A、B,l1∥l2,求证:O在AB上.
证明:连结OA,并延长交l2于B′,
∵l1切⊙O于点A,∴OA⊥l1.又∵l1∥l2,
∴OA⊥l2,即OB′⊥l2.
∴B为l2与⊙O的切点.∴OB⊥l2.
但过O只有一条直线与l2垂直.∴B′与B重合.
即A、O、B在一条直线上,或AB经过点O.
名校课堂系列答案