题目内容
定义在 上的偶函数
上的偶函数 满足条件
满足条件 ,且在
,且在 上递减,若
上递减,若 是锐角三角形的两内角,以下关系成立的是
是锐角三角形的两内角,以下关系成立的是
 上的偶函数
上的偶函数 满足条件
满足条件 ,且在
,且在 上递减,若
上递减,若 是锐角三角形的两内角,以下关系成立的是
是锐角三角形的两内角,以下关系成立的是A. | B. |
C. | D. |
B
分析:由题设条件可以得出偶函数f(x)在[-1,0]减,在[0,1]增,根据α,β是锐角三角形的两内角比较出其函数值大小就可根据函数的单调性找出正确选项
解答:解:∵定义在R上的偶函数f(x)满足条件f(x+2)=f(x),且在[-3,-2]上递减,
∴f(x)在[-1,0]减,在[0,1]增,
又α,β是锐角三角形的两内角,
∴α+β> ,即α>
,即α> -β,β>
-β,β> -α
-α
∴0<sin( -β)<sinα<1,0<sin(
-β)<sinα<1,0<sin( -α)<sinβ<1
-α)<sinβ<1
∴0<cosβ<sinα<1,0<cosα<sinβ<1
∴f(cosβ)<f(sinα),f(cosα)<f(sinβ)
考察四个选项,B符合要求
故选B
解答:解:∵定义在R上的偶函数f(x)满足条件f(x+2)=f(x),且在[-3,-2]上递减,
∴f(x)在[-1,0]减,在[0,1]增,
又α,β是锐角三角形的两内角,
∴α+β>
 ,即α>
,即α> -β,β>
-β,β> -α
-α∴0<sin(
 -β)<sinα<1,0<sin(
-β)<sinα<1,0<sin( -α)<sinβ<1
-α)<sinβ<1∴0<cosβ<sinα<1,0<cosα<sinβ<1
∴f(cosβ)<f(sinα),f(cosα)<f(sinβ)
考察四个选项,B符合要求
故选B

练习册系列答案
相关题目
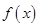 满足
满足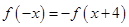 ,当
,当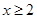 时,
时,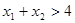 ,且
,且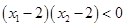 ,则
,则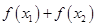 的值为( )
的值为( )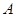 恒小于
恒小于
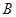 恒大于
恒大于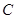 可能为
可能为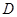 可正可负
可正可负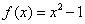 ,对任意
,对任意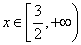 ,
,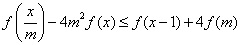 恒成立,求:实数
恒成立,求:实数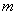 的取值范围。
的取值范围。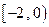 ∪
∪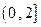 上的奇函数,当
上的奇函数,当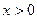 时,f (x)的图象如图所示,那么f (x)的值域是
时,f (x)的图象如图所示,那么f (x)的值域是 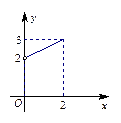
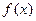 是定义在R上的增函数,且
是定义在R上的增函数,且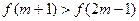 ,
,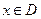 ,均有
,均有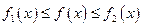 成立,则称函数
成立,则称函数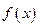 为函数
为函数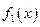 到函数
到函数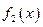 在区间
在区间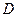 上的“折中函数”.已知函数
上的“折中函数”.已知函数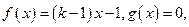
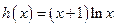 ,且
,且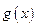 到
到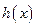 在区间
在区间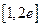 上的“折中函数”,则实数
上的“折中函数”,则实数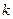 的取值范围为 ▲ .
的取值范围为 ▲ .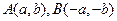 在函数
在函数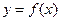 的图象上,
的图象上,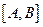 为函数
为函数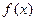 的一组关于原点的中心对称点(
的一组关于原点的中心对称点(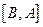 看作一组).
看作一组).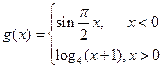 关于原点的中心对称点的组数为 ▲ .
关于原点的中心对称点的组数为 ▲ . 满足
满足  ,当
,当 时,
时, ,则
,则 在
在 上零点的个数为 ( )
上零点的个数为 ( ) .1005 C.2009 D.2010
.1005 C.2009 D.2010 >0,
>0, >0,函数
>0,函数 ”的是( )
”的是( )