题目内容
已知A、B为抛物线C:y2 = 4x上的两个动点,点A在第一象限,点B在第四象限l1、l2分别过点A、B且与抛物线C相切,P为l1、l2的交点.
(1)若直线AB过抛物线C的焦点F,求证:动点P在一条定直线上,并求此直线方程;
(2)设C、D为直线l1、l2与直线x = 4的交点,求 面积的最小值.
面积的最小值.
(1)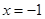 ;(2)
;(2)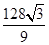
解析试题分析:(1)设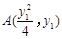 ,
, 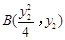 (
(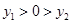 ),
),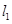 方程为
方程为 ,与抛物线方程联立,利用直线
,与抛物线方程联立,利用直线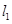 与抛物线y2 = 4x相切,故
与抛物线y2 = 4x相切,故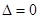 ,求
,求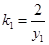 ,故切线
,故切线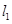 的方程
的方程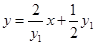 。同理可求得切线
。同理可求得切线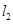 方程为
方程为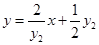 ,联立得交点
,联立得交点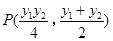 ,再注意到已知条件直线AB过抛物线C的焦点F,故表示直线AB的方程为
,再注意到已知条件直线AB过抛物线C的焦点F,故表示直线AB的方程为 ,将抛物线焦点
,将抛物线焦点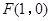 代入,得
代入,得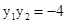 ,从而发现点P横坐标为
,从而发现点P横坐标为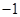 ,故点P在定直线
,故点P在定直线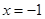 上;(2)列
上;(2)列 面积关于某个变量的函数关系式,再求函数最小值即可,由已知得,
面积关于某个变量的函数关系式,再求函数最小值即可,由已知得,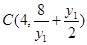 ,
,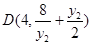 ,故
,故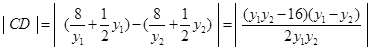 ,又高为
,又高为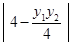 ,故三角形
,故三角形 的面积为
的面积为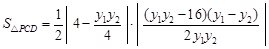 ,再求最小值即可.
,再求最小值即可.
(1)设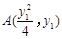 ,
, 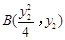 (
(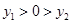 ).
).
易知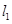 斜率存在,设为
斜率存在,设为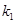 ,则
,则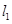 方程为
方程为 .
.
由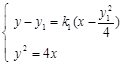 得,
得,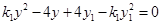 ①
①
由直线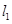 与抛物线
与抛物线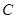 相切,知
相切,知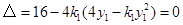 .
.
于是,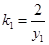 ,
,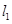 方程为
方程为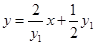 .
.
同理,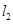 方程为
方程为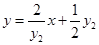 .
.
联立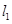 、
、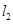 方程可得点
方程可得点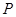 坐标为
坐标为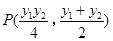 ,
,
∵ 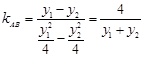 ,
,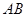 方程为
方程为 ,
,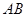 过抛物线
过抛物线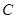 的焦点
的焦点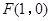 .
.
∴ ,∴
,∴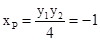 ,点P在定直线
,点P在定直线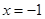 上.
上.
(2)由(1)知,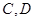 的坐标分别为
的坐标分别为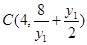 ,
,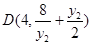
∴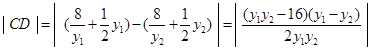 .
.
∴ 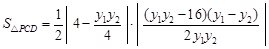 .
.
设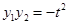 (
(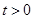 ),
),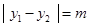 ,
,
由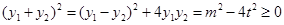 知,
知,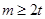 ,当且仅当
,当且仅当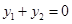 时等号成立.
时等号成立.
∴ 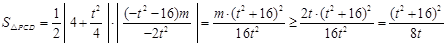

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图),双曲线
的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图),双曲线 过点P且离心率为
过点P且离心率为 .
. 的方程;
的方程; 过点P且与
过点P且与 过
过
 中,原点为
中,原点为 ,抛物线
,抛物线 的方程为
的方程为 ,线段
,线段 是抛物线
是抛物线 ;
; ,求证:直线
,求证:直线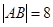 时,设圆
时,设圆 ,若存在且仅存在两条动弦
,若存在且仅存在两条动弦 相切,求半径
相切,求半径 的取值范围?
的取值范围?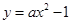 ,直线
,直线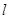 的方程为
的方程为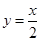 ,点
,点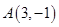 关于直线
关于直线 ,求过点
,求过点 及抛物线与
及抛物线与 轴两个交点的圆的方程;
轴两个交点的圆的方程;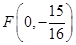 是抛物线的焦点,
是抛物线的焦点, 是抛物线上的动点,求
是抛物线上的动点,求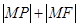 的最小值及此时点
的最小值及此时点 ,
, 、
、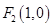 是椭圆的左右焦点,且椭圆经过点
是椭圆的左右焦点,且椭圆经过点 .
. 且倾斜角等于
且倾斜角等于 的直线
的直线 ,交椭圆于
,交椭圆于 、
、 两点,求
两点,求 的面积.
的面积.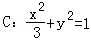 .如图所示,斜率为k(k>0)且不过原点的直线l交椭圆C于A,B两点,线段AB的中点为E,射线OE交椭圆C于点G,交直线x=﹣3于点D(﹣3,m).
.如图所示,斜率为k(k>0)且不过原点的直线l交椭圆C于A,B两点,线段AB的中点为E,射线OE交椭圆C于点G,交直线x=﹣3于点D(﹣3,m).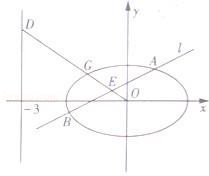
 ,
, 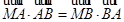 ,M点的轨迹为曲线C。
,M点的轨迹为曲线C。 与抛物线
与抛物线 交于两点A、B,如果弦
交于两点A、B,如果弦 的长度
的长度 .
. 的值;
的值; (O为原点)。
(O为原点)。