题目内容
已知直线y=k(x+2)(k>0)与抛物线C:y2=8x相交于A、B两点,F为C的焦点,若|FA|=2|FB|,则k等于( )
(A)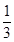 (B)
(B) 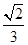 (C)
(C) 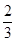 (D)
(D) 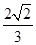
(A)
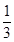 (B)
(B) 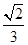 (C)
(C) 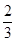 (D)
(D) 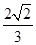
D
将y=k(x+2)代入y2=8x,得
k2x2+(4k2-8)x+4k2=0.
设交点的横坐标分别为xA,xB,
则xA+xB= -4,①
-4,①
xA·xB=4.
又|FA|=xA+2,|FB|=xB+2,
|FA|=2|FB|,
∴2xB+4=xA+2.
∴xA=2xB+2.②
∴将②代入①得xB= -2,
-2,
xA= -4+2=
-4+2= -2.
-2.
故xA·xB= =4.
=4.
解之得k2= .
.
而k>0,∴k=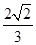 ,满足Δ>0.故选D.
,满足Δ>0.故选D.
k2x2+(4k2-8)x+4k2=0.
设交点的横坐标分别为xA,xB,
则xA+xB=
 -4,①
-4,①xA·xB=4.
又|FA|=xA+2,|FB|=xB+2,
|FA|=2|FB|,
∴2xB+4=xA+2.
∴xA=2xB+2.②
∴将②代入①得xB=
 -2,
-2,xA=
 -4+2=
-4+2= -2.
-2.故xA·xB=
 =4.
=4.解之得k2=
 .
.而k>0,∴k=
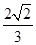 ,满足Δ>0.故选D.
,满足Δ>0.故选D.
练习册系列答案
相关题目
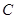 上任意一点
上任意一点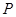 作直线
作直线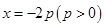 的垂线,垂足为
的垂线,垂足为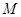 ,且
,且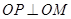 .
.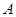 、
、 是曲线
是曲线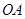 和
和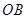 的倾斜角分别为
的倾斜角分别为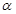 和
和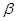 ,
,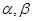 变化且
变化且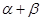 为定值
为定值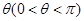 时,证明直线
时,证明直线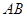 恒过定点,
恒过定点, 上一点
上一点 与该抛物线的焦点
与该抛物线的焦点 的距离
的距离 ,则点
,则点 ,过焦点
,过焦点 的直线交抛物线于
的直线交抛物线于 两点,线段
两点,线段 的中点的横坐标为
的中点的横坐标为 ,
, =_____________.
=_____________. 的垂线,垂足为M,则∠MAF的平分线所在直线的方程为 .
的垂线,垂足为M,则∠MAF的平分线所在直线的方程为 . 的顶点F是抛物线
的顶点F是抛物线 的焦点,顶点B在抛物线的准线
的焦点,顶点B在抛物线的准线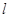 上且
上且 ⊥
⊥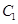 开口内
开口内 值有关
值有关