题目内容
若集合M={y|y=2x,x∈R},集合S={x|y=lg(x-1)},则下列各式中正确的是
- A.M∪S=M
- B.M∪S=S
- C.M=S
- D.M∩S=Φ
A
分析:根据题意,由指数函数与对数函数的性质,可得M={y|y>0}、S={x|x>1},再由并集的求法可得答案.
解答:根据题意,M为y=2x的值域,由指数函数的性质,可得M={y|y>0},
S为y=lg(x-1)的定义域,由对数函数的定义域,必有x-1>0,即S={x|x>1},
则M∪S={y|y>0}=M,
故选A.
点评:解本题时,应注意集合的表示方法,S与M都是数集,与其代表元素(x,y)无关.
分析:根据题意,由指数函数与对数函数的性质,可得M={y|y>0}、S={x|x>1},再由并集的求法可得答案.
解答:根据题意,M为y=2x的值域,由指数函数的性质,可得M={y|y>0},
S为y=lg(x-1)的定义域,由对数函数的定义域,必有x-1>0,即S={x|x>1},
则M∪S={y|y>0}=M,
故选A.
点评:解本题时,应注意集合的表示方法,S与M都是数集,与其代表元素(x,y)无关.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
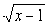 },则M∩P等于 ( )
},则M∩P等于 ( ) ,则M∩P=( )
,则M∩P=( ) ,则M∩P=( )
,则M∩P=( ) ,则M∩P=( )
,则M∩P=( )