题目内容
(本小题满分12分)
设二次函数![]() ,对任意实数
,对任意实数![]() ,有
,有![]() 恒成立;数列
恒成立;数列![]() 满足
满足![]() .
.
(1)求函数![]() 的解析式和值域;
的解析式和值域;
(2)试写出一个区间![]() ,使得当
,使得当![]() 时,数列
时,数列![]() 在这个区间上是递增数列,并说明理由;
在这个区间上是递增数列,并说明理由;
(3)已知![]() ,是否存在非零整数
,是否存在非零整数![]() ,使得对任意
,使得对任意![]() ,都有
,都有
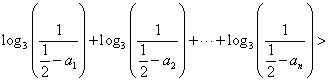
![]() 恒成立,若存在,求之;若不存在,说明理由.
恒成立,若存在,求之;若不存在,说明理由.
解:(1)由![]() 恒成立等价于
恒成立等价于![]() 恒成立,
恒成立,
从而得: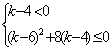 ,化简得
,化简得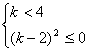 ,从而得
,从而得![]() ,所以
,所以![]() ,
,
其值域为![]() .
.
(2)解:当![]() 时,数列
时,数列![]() 在这个区间上是递增数列,证明如下:
在这个区间上是递增数列,证明如下:
设![]() ,则
,则![]() ,所以对一切
,所以对一切![]() ,均有
,均有![]() ;
; ![]()
![]() ,从而得
,从而得![]() ,即
,即![]() ,所以数列
,所以数列![]() 在区间
在区间![]() 上是递增数列.
上是递增数列.
注:本题的区间也可以是![]() 、
、![]() 、
、![]() 等无穷多个.
等无穷多个.
另解:若数列![]() 在某个区间上是递增数列,则
在某个区间上是递增数列,则![]()
即![]()
![]() 又当
又当![]() 时,
时,![]() ,所以对一切
,所以对一切![]() ,均有
,均有![]() 且
且![]() ,所以数列
,所以数列![]() 在区间
在区间![]() 上是递增数列.
上是递增数列.
(3)由(2)知![]() ,从而
,从而![]() ;
;
![]() ,即
,即![]() ;………12分
;………12分
令![]() ,则有
,则有![]() 且
且![]() ;
;
从而有![]() ,可得
,可得![]() ,所以数列
,所以数列![]() 是
是![]() 为首项,公比为
为首项,公比为![]() 的等比数列,从而得
的等比数列,从而得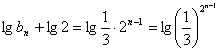 ,即
,即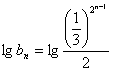 ,所以
,所以 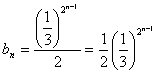 ,
,
所以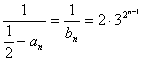 ,所以
,所以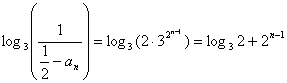 ,
,
所以,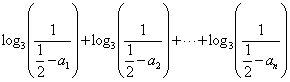
![]() .
.
即![]()
![]()
![]() ,所以,
,所以,![]() 恒成立
恒成立
当![]() 为奇数时,即
为奇数时,即![]() 恒成立,当且仅当
恒成立,当且仅当![]() 时,
时,![]() 有最小值
有最小值![]() 为。
为。![]()
当![]() 为偶数时,即
为偶数时,即![]() 恒成立,当且仅当
恒成立,当且仅当![]() 时,有最大值
时,有最大值![]() 为。
为。![]()
所以,对任意![]() ,有
,有![]() 。又
。又![]() 非零整数,
非零整数,![]()


练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目