题目内容
设函数f(x)=x3-2ex2+mx-lnx,记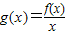 ,若函数g(x)至少存在一个零点,则实数m的取值范围是 .
,若函数g(x)至少存在一个零点,则实数m的取值范围是 .
【答案】分析:由题意得:x2-2ex+m-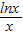 =0有解,即m=-x2+2ex+
=0有解,即m=-x2+2ex+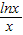 ,我们画出函数 y=-x2+2ex+
,我们画出函数 y=-x2+2ex+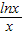 的图象,根据图象分析函数存在零点时m的取值范围,进而求出实数m的取值范围,即可得到答案.
的图象,根据图象分析函数存在零点时m的取值范围,进而求出实数m的取值范围,即可得到答案.
解答: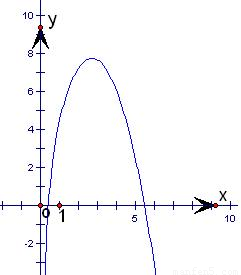 解:∵函数g(x)至少存在一个零点,
解:∵函数g(x)至少存在一个零点,
∴x2-2ex+m-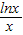 =0有解,即m=-x2+2ex+
=0有解,即m=-x2+2ex+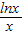 ,
,
画出函数y=-x2+2ex+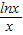 的图象如下图所示:
的图象如下图所示:
则若函数g(x)至少存在一个零点,
则m小于函数y=-x2+2ex+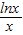 的最大值即可,
的最大值即可,
函数y=-x2+2ex+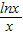 的最大值为:
的最大值为: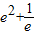
即m≤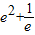 .
.
故答案为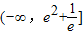 .
.
点评:本题考查的知识点是函数零点的判定定理,数形结合思想是解析函数图象交点个数、函数零点个数中最常用的方法,即画出满足条件的图象,然后根据图象直观的分析出答案,但数形结合的前提是熟练掌握各种基本初等函数的图象和性质.
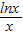 =0有解,即m=-x2+2ex+
=0有解,即m=-x2+2ex+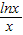 ,我们画出函数 y=-x2+2ex+
,我们画出函数 y=-x2+2ex+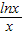 的图象,根据图象分析函数存在零点时m的取值范围,进而求出实数m的取值范围,即可得到答案.
的图象,根据图象分析函数存在零点时m的取值范围,进而求出实数m的取值范围,即可得到答案.解答:
 解:∵函数g(x)至少存在一个零点,
解:∵函数g(x)至少存在一个零点,∴x2-2ex+m-
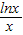 =0有解,即m=-x2+2ex+
=0有解,即m=-x2+2ex+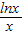 ,
,画出函数y=-x2+2ex+
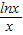 的图象如下图所示:
的图象如下图所示:则若函数g(x)至少存在一个零点,
则m小于函数y=-x2+2ex+
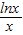 的最大值即可,
的最大值即可,函数y=-x2+2ex+
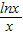 的最大值为:
的最大值为: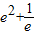
即m≤
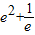 .
.故答案为
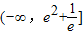 .
.点评:本题考查的知识点是函数零点的判定定理,数形结合思想是解析函数图象交点个数、函数零点个数中最常用的方法,即画出满足条件的图象,然后根据图象直观的分析出答案,但数形结合的前提是熟练掌握各种基本初等函数的图象和性质.

练习册系列答案
相关题目