题目内容
已知 ,记
,记
求(1)
 的值;
的值;(2)函数f(x)的最小值及相应的x值.
【答案】分析:(1)利用两个向量的数量积公式可得  =(sinx,sinx)•(cosx,sinx)=sinxcosx+sin2x,把x=
=(sinx,sinx)•(cosx,sinx)=sinxcosx+sin2x,把x= 代入运算求得结果.
代入运算求得结果.
(2)利用两角差的正弦公式把函数f(x)化为 +
+ sin(2x-
sin(2x- ),故当2x-
),故当2x- =2kπ+
=2kπ+ 时,函数f(x)有最小值等于
时,函数f(x)有最小值等于 .
.
解答:解:(1) =(sinx,sinx)•(cosx,sinx)=sinxcosx+sin2x,
=(sinx,sinx)•(cosx,sinx)=sinxcosx+sin2x,
∴ =sin
=sin cos
cos +
+ =
= +
+ =
= .
.
(2)函数f(x)= +
+ =
= +
+ sin(2x-
sin(2x- ),
),
故当2x- =2kπ+
=2kπ+ 时,函数f(x)有最小值等于
时,函数f(x)有最小值等于 =
= .
.
点评:本题考查两个向量的数量积公式,两角差的正弦公式的应用,把函数f(x)化为 +
+ sin(2x-
sin(2x- ),是解题的关键.
),是解题的关键.
 =(sinx,sinx)•(cosx,sinx)=sinxcosx+sin2x,把x=
=(sinx,sinx)•(cosx,sinx)=sinxcosx+sin2x,把x= 代入运算求得结果.
代入运算求得结果.(2)利用两角差的正弦公式把函数f(x)化为
 +
+ sin(2x-
sin(2x- ),故当2x-
),故当2x- =2kπ+
=2kπ+ 时,函数f(x)有最小值等于
时,函数f(x)有最小值等于 .
.解答:解:(1)
 =(sinx,sinx)•(cosx,sinx)=sinxcosx+sin2x,
=(sinx,sinx)•(cosx,sinx)=sinxcosx+sin2x,∴
 =sin
=sin cos
cos +
+ =
= +
+ =
= .
.(2)函数f(x)=
 +
+ =
= +
+ sin(2x-
sin(2x- ),
),故当2x-
 =2kπ+
=2kπ+ 时,函数f(x)有最小值等于
时,函数f(x)有最小值等于 =
= .
.点评:本题考查两个向量的数量积公式,两角差的正弦公式的应用,把函数f(x)化为
 +
+ sin(2x-
sin(2x- ),是解题的关键.
),是解题的关键. 
练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
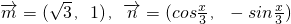 ,记
,记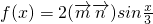 .
.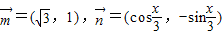 ,记
,记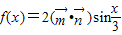 .
.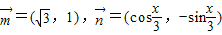 ,记
,记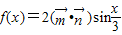 .
. ,记
,记
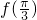 的值;
的值;