题目内容
已知 为等比数列
为等比数列 的前
的前 项和,
项和,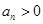 ,
, ,前
,前 项中的数值最大的项为54,求
项中的数值最大的项为54,求
解: ,
,
而 ,所以数列
,所以数列 是递增的数列,前
是递增的数列,前 项中的数值最大的项为
项中的数值最大的项为 ,故
,故
 ,
,
解析试题分析由 列方程解出首和公比。
列方程解出首和公比。
考点;等比数列通项及前n项和.
点评:本题考查了等比数列通项及前n项和,列方程是解题的关键,注意q>1.

练习册系列答案
相关题目
已知等差数列 满足
满足 ,
, ,
, ,
, ,则
,则 的值为( )
的值为( )
A.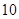 | B.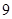 | C. | D. |
已知实数等比数列{an}的前n项和为Sn,则下列结论一定成立的是( )
A.若 ,则 ,则 |
B.若 ,则 ,则 |
C.若 ,则 ,则 |
D.若 ,则 ,则 |
设 是各项为正数的等比数列,
是各项为正数的等比数列, 是其公比,
是其公比, 是其前
是其前 项的积,且
项的积,且 ,则下列结论错误的是( )
,则下列结论错误的是( )
A. | B. |
C. | D. 与 与 均为 均为 的最大值 的最大值 |
数列-1, ,-
,- ,
, ,…的一个通项公式是( )
,…的一个通项公式是( )
A. | B. |
C. | D. |
已知 是定义在
是定义在 上的偶函数,且在
上的偶函数,且在 上是增函数,设
上是增函数,设 ,
, ,
, ,则
,则 的大小关系是( )
的大小关系是( )
A. | B. | C. | D. |
某几何体的三视图如图所示,则该几何体的体积为( )
| A.10 | B.20 | C.40 | D.60 |
 中,角
中,角 的对边分别是
的对边分别是 ,若
,若 的面积为
的面积为 ,则
,则 ;
;
 。
。