题目内容
设函数
的图象为C，①图象C关于直线
对称；②函数f（x）在区间
内是增函数；③由y=3sin2x的图象向右平移
个单位长度可以得到图象C以上三个论断中，正确论断的个数是（ ）
A．0
B．1
C．2
D．3
【答案】分析：利用y=Asin（ωx+?）的对称轴是令ωx+?=
，k∈Z，解得的x 的值，单调区间是令ωx+?∈[-
+2kπ，
+2kπ]，求得的x的范围，以及图象变换，逐一判断三个论断，即可得到正确论断的个数．
解答：解：
的对称轴为2x-
=
，k∈Z的解，
即对称轴为x=
，k∈Z，当k=1时，对称轴为x=
，∴①正确．
的增区间为不等式-
+2kπ≤2x-
≤
+2kπ的解集，
即增区间为[-
+kπ，
+kπ]，k∈Z，
在这个范围内，∴②正确．
由y=3sin2x的图象向右平移
个单位长度可以得到函数y=3sin（2x-
）的图象，∴③错误
故选C
点评：本题主要考查y=Asin（ωx+?）的对称轴，单调区间，图象的求法，属于常规题．
，k∈Z，解得的x 的值，单调区间是令ωx+?∈[-+2kπ，+2kπ]，求得的x的范围，以及图象变换，逐一判断三个论断，即可得到正确论断的个数．解答：解：
的对称轴为2x-=，k∈Z的解，即对称轴为x=
，k∈Z，当k=1时，对称轴为x=，∴①正确．的增区间为不等式-+2kπ≤2x-≤+2kπ的解集，即增区间为[-
+kπ，+kπ]，k∈Z，在这个范围内，∴②正确．由y=3sin2x的图象向右平移
个单位长度可以得到函数y=3sin（2x-）的图象，∴③错误故选C
点评：本题主要考查y=Asin（ωx+?）的对称轴，单调区间，图象的求法，属于常规题．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
的图象为C，
对称；
内是增函数；
个单位长度可以得到图象C
的图象为C，给出下列命题：
对称；
内是增函数；
对称．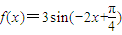
的图象为C，有下列四个命题：
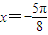对称：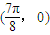
；
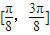上是增函数；
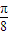得到．其中真命题的序号是 ．
的图象为C，C关于直线
的对称图象为D，再将D向右平移2个单位，得到图象E，则E的表达式是 
C．
D．