Question

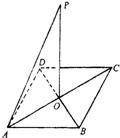已知边长分别为a米和b米的矩形球场ABCD，在球场正中的上方悬挂一照明灯P，已知球场上各点照明亮度与灯光照射到这点光线和地面夹角的正弦成正比，与这点到灯的距离的平方成反比，若要使球场最边缘的点A获得最好的照明亮度，灯距地面的高度应为多少米？

Answer 1

分析：设∠PAO=θ，照明亮度为Q，则由题意得出照明亮度的函数关系式，再利用导数求出函数Q的最大值即可，从而得出若要使球场最边缘的点A获得最好的照明亮度，灯距地面的高度应为多少米．

解答：解：设∠PAO=θ，照明亮度为Q，
则Q=k•

sinθ

AP2

=k•

sinθcos2θ

OA 2

令y=sinθcos²θ=sinθ（1-sin²θ）=-sin³θ+sinθ
设sinθ=t，则y=-t³+t
y'=-3t²+1=0，解得t=

3

3

即sinθ=

3

3

，则tanθ=

2

2

∴当t=

3

3

时Q取最大值
而OA=

a2+b2

2

此时OP=OA•tanθ=

a2+b2

2

×

2

2

=

2(a2+b2)

4

答：若要使球场最边缘的点A获得最好的照明亮度，灯距地面的高度应为

2(a2+b2)

4

米．

点评：本题主要考查了空间想象能力，实际应用能力和建模能力，以及利用导数求函数的最值等有关知识，属于难题．