题目内容
下列四组函数中表示同一函数的是( )
A. , , | B. |
C. , , | D. , , |
C
解析试题分析:要判断两个函数是否是同一个函数,需要从三个方面来分析,即定义域,对应法则和值域,观察四个选项结果有三个的定义域不同,只有选C.解:要判断两个函数是否是同一个函数,需要从三个方面来分析,即定义域,对应法则和值域,对于A选项,f(x)的定义域为R,g(x)的定义域为{x|x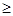 ≠0},∴不是同一函数.对于B选项,
≠0},∴不是同一函数.对于B选项, 对应法则不同,∴不是同一函数,对于C选项,f(x)的定义域为R,g(x)的定义域为R,且两函数解析式化简后为同一解析式,∴是同一函数,对于D选项,f(x)的定义域为R,g(x)的定义域为x=1,∴不是同一函数,故选C.
对应法则不同,∴不是同一函数,对于C选项,f(x)的定义域为R,g(x)的定义域为R,且两函数解析式化简后为同一解析式,∴是同一函数,对于D选项,f(x)的定义域为R,g(x)的定义域为x=1,∴不是同一函数,故选C.
考点:同一函数
点评:本题考查判断两个函数是否是同一函数,在开始学习函数的概念时,这是经常出现的一个问题,注意要从三个方面来分析.

练习册系列答案
相关题目
已知函数 的定义域为
的定义域为 ,则函数
,则函数 的定义域为( )
的定义域为( )
A. | B. | C. | D. |
设 则不等式
则不等式 的解集为( )
的解集为( )
| A.(1,2)∪(3,+∞) | B.( ,+∞) ,+∞) |
C.(1,2)∪( ,+∞) ,+∞) | D.(1,2) |
函数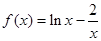 的零点所在的大致区间是 ( )
的零点所在的大致区间是 ( )
A.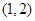 | B.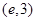 | C.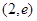 | D.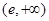 |
设 是方程
是方程 的解,则
的解,则 属于区间 ( )
属于区间 ( )
| A.(0,1) | B.(1,2) | C.(2,3) | D.(3,4) |
已知f(x)是以2为周期的偶函数,当x∈[0, 1]时,f(x)=x,那么在区间[-1,3]内关于x的方程f(x)=kx+k+1(k∈R,k≠-1)的根的个数
| A.不可能有3个 | B.最少有1个,最多有4个 |
| C.最少有1个,最多有3个 | D.最少有2个,最多有4个 |
函数 是( )
是( )
| A.奇函数 | B.偶函数 |
| C.既是奇函数又是偶函数 | D.既不是奇函数也不是偶函数 |
已知函数 为奇函数,且当
为奇函数,且当 时,
时, ,则
,则 ( )
( )
A. | B. | C. | D. |
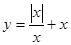 的图象是( )
的图象是( )