Question

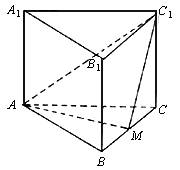
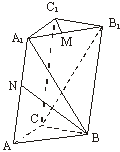
18.（甲）如图，直三棱柱ABC－A₁B₁C₁，底面△ABC中，CA＝CB＝1，∠BCA=，

棱AA₁＝2，M、N分别是A₁B₁、A₁A的中点.

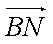
（Ⅰ）求的长；

（Ⅱ）求cos＜＞的值；

（Ⅲ）求证A₁B⊥C₁M.

Answer 1

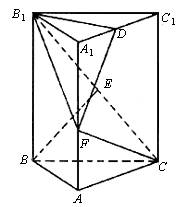
18.（甲）本小题主要考查空间向量及运算的基本知识.

如图，以C为原点建立空间直角坐标系O－xyz.

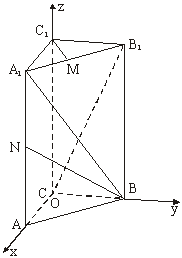
（Ⅰ）解：依题意得B（0，1，0），N（1，0，1）.

　　　　 ∴｜｜＝＝.        

　

（Ⅱ）解：依题意得A₁（1，0，2），B（0，1，0），C（0，0，0），B₁（0，1，2）.

　∴＝（1，－1，2），＝（0，1，2）.

　      ·＝3，｜｜＝，｜｜＝.                  

      ∴cos＜，＞＝＝.       

　

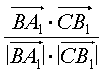（Ⅲ）证明：依题意得C₁（0，0，2），M（，，2），

　       ＝（－1，1，－2），＝（，，0），

　       ∴·＝－＋＋0＝0，∴⊥，

　       ∴A₁B⊥C₁M.                                                        

 

【参考解法】

　　（Ⅱ）【定理】如图.已知：两条异面直线AE、BF上，点A、E∈AE，点B、F∈BF，∠AEF=α，

∠BFE＝β，二面角A—EF—B为θ，异面直线AE、BF所成角为，（0°＜≤90°）。则

＝arc cos|sinα·sinβ·cosθ－cosα·cosβ|

 （引自：《中等数学实用定理选讲》书，上海科技出版社。）

　解：令二面解A₁－BB₁－C为θ，显然θ＝45°∠A₁BB₁＝α，∠BB₁C＝β，则

cos<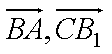>=|sin sin－cos cos|

在△A₁BB₁中，A₁B₁＝，BB₁＝2，A₁B＝，∠BB₁A_1＝，

∴sin==，cos=

在△BB₁C中，BB₁＝2，BC＝1，B₁C＝，∠BB₁C＝，

∴sin=.cos=

∴cos<>=|－|=.