Question

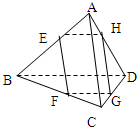
E，F，G，H分别是空间四边形ABCD的边AB，BC，CD，DA的中点，则AC与平面EFGH的位置关系是

平行

．

Answer 1

分析：根据三角形的中位线定理，可证出四边形EFGH是平行四边形，再利用线面平行的判定可得结论．

解答：证明：∵空间四边形ABCD中，E，F分别是AB，BC的中点，
∴EF是△ABD的中位线，所以EF∥AC，且EF=

1

2

AC．
同理，HG∥AC，且HG=

1

2

AC
所以EF∥HG，且EF=HG．
所以四边形EFGH为平行四边形．
∵EF∥AC，EF?平面EFGH，AC?平面EFGH
∴AC∥平面EFGH
故答案为：平行

点评：本题考查三角形中位线的性质，考查线面位置关系，属于中档题．