题目内容
对于任意两个正整数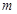 、
、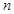 ,定义某种运算“※”,法则如下:当
,定义某种运算“※”,法则如下:当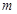 、
、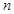 都是正奇数时,
都是正奇数时,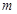 ※
※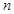 =
=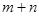 ;当
;当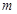 、
、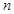 不全为正奇数时,
不全为正奇数时,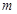 ※
※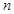 =
=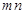 .则在此定义下,集合
.则在此定义下,集合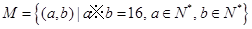 中的元素个数是( )
中的元素个数是( )
A.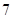 | B.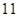 | C.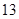 | D.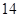 |
C
解析试题分析:从定义出发,抓住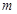 、
、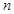 的奇偶性对
的奇偶性对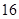 实行分拆是解决本题的关键,当
实行分拆是解决本题的关键,当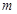 、
、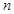 同奇时,根据
同奇时,根据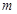 ※
※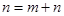 将
将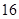 分拆两个同奇数的和,有
分拆两个同奇数的和,有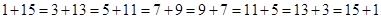 ,共有
,共有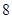 对;当
对;当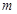 、
、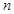 不全为奇数时,根据
不全为奇数时,根据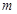 ※
※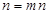 将
将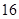 分拆两个不全为奇数的积,再算其组数即可,此时有
分拆两个不全为奇数的积,再算其组数即可,此时有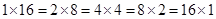 ,共
,共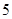 对.
对.
∴共有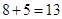 个,故选C.
个,故选C.
考点:考查分析问题的能力以及集合中元素的性质.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
已知全集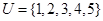 ,集合
,集合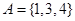 ,集合
,集合 ,则
,则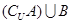 为 ( )
为 ( )
A.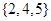 | B.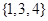 | C.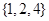 | D.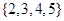 |
设集合M= ,N=
,N=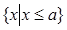 ,若
,若 ,则
,则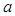 的取值范围是 ( )
的取值范围是 ( )
A.(? ,1) ,1) | B.(?∞,1] | C.[1,+∞) | D.(2,+∞) |
设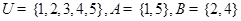 ,则
,则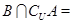 ( ).
( ).
A.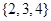 | B.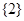 | C.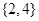 | D.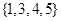 |
定义一个集合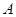 的所有子集组成的集合叫做集合
的所有子集组成的集合叫做集合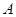 的幂集,记为
的幂集,记为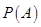 ,用
,用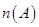 表示有限集
表示有限集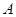 的元素个数,给出下列命题:①对于任意集合
的元素个数,给出下列命题:①对于任意集合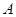 ,都有
,都有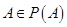 ;②存在集合
;②存在集合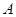 ,使得
,使得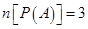 ;
;
③用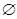 表示空集,若
表示空集,若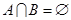 ,则
,则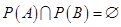 ;④若
;④若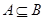 ,则
,则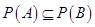 ;⑤若
;⑤若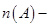
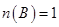 ,则
,则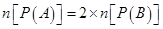 其中正确的命题个数为( )
其中正确的命题个数为( )
A.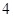 | B.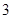 | C. | D. |
设集合 ,
, ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
已知集合A={0,1,2},则集合B={x﹣y|x∈A,y∈A}中元素的个数是( )
| A.1 | B.3 | C.5 | D.9 |
已知集合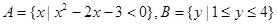 ,则下列结论正确的是( )
,则下列结论正确的是( )
A.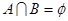 |
B.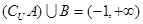 |
C. |
D.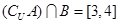 |
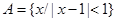 ,
, 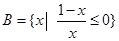 ,则A∩(∁U B)=( )
,则A∩(∁U B)=( )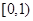 C.(1, 2) D. (0,2)
C.(1, 2) D. (0,2)