Question

已知二次函数f(x)对任意，都有f(1－x)＝f(1＋x)成立，设向量a＝(sinx，2)，b＝(2sinx，)，c＝(cos2x，1)，d＝(1，2)，当[0，π]时，求不等式f(a·b)＞f(c·d)的解集．

Answer 1

答案：
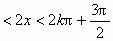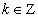解析：

　　设f(x)的二次项系数为m，其图象上两点为(1－x，)、B(1＋x，)

　　因为，，所以，

　　由x的任意性得f(x)的图象关于直线x＝1对称，

　　若m＞0，则x≥1时，f(x)是增函数，若m＜0，则x≥1时，f(x)是减函数．

　　∵，，，，，

　　∴当时，

，．

　　∵，

　　∴．

　　当时，同理可得或．

　　综上：的解集是当时，为；

　　当时，为，或．