题目内容
甲,乙,丙3人投篮,投进的概率分别是![]() 现3人各投篮1次,求:
现3人各投篮1次,求:
(Ⅰ)现有3人各投篮1次,求3人都没有投进的概率;
(Ⅱ)用ξ表示乙投篮3次的进球数,求随机变量ξ的概率分布及数学期望Eξ.
解析:(I)记“甲投篮1次投进”为事件A1,“乙投蓝1次投进”为事件A2,“丙投篮1次投进”为事件A3,“3人都没有投进”为事件A.则![]()
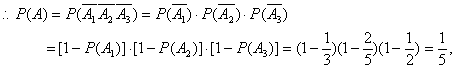
∴3人都没有投进的概率为![]() .
.
(II)解法一: 随机变量ξ的可能值有0,1,2,3.则Eξ=np=3×![]() =
=![]() .
.
解法二:ξ的概率分布为
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
Eξ=0×![]() +1×
+1×![]() +2×
+2×![]() +3×
+3×![]() =
=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
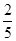 ,
, ,
, .
现3人各投篮1次,
.
现3人各投篮1次,