题目内容
已知函数y=f(x)是定义在R上的奇函数,当x≤0时,f(x)=2x+x2,若存在正数a,b,使得当x∈[a,b]时,f(x)的值域为[ ],则a+b=
],则a+b=
 ],则a+b=
],则a+b=| A.1 | B. | C. | D. |
D
设 则
则 于是
于是 又函数
又函数 是奇函数,所以
是奇函数,所以
 且
且

 时,
时, 因此根据题意可知:
因此根据题意可知: ,所以函数在
,所以函数在 上是减函数;则
上是减函数;则 由方程
由方程 得:
得:
 ,
,
 解得
解得 (舍去);同样
(舍去);同样 又
又
则 故选D
故选D
 则
则 于是
于是 又函数
又函数 是奇函数,所以
是奇函数,所以
 且
且

 时,
时, 因此根据题意可知:
因此根据题意可知: ,所以函数在
,所以函数在 上是减函数;则
上是减函数;则 由方程
由方程 得:
得: ,
,
 解得
解得 (舍去);同样
(舍去);同样 又
又
则
 故选D
故选D
练习册系列答案
相关题目
 且
且 ,若
,若 ,则
,则 的取值范围是( )
的取值范围是( )



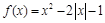 的图像,并写出该函数的单调区间与值域。
的图像,并写出该函数的单调区间与值域。 的解析式写成分段函数;
的解析式写成分段函数;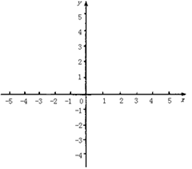
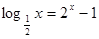 的实数根的个数为( )
的实数根的个数为( ) 的坐标
的坐标 ,
, 满足
满足 ,则
,则 的最大值是
的最大值是 、
、
 、
、
 、
、
 、
、
 上的偶函数
上的偶函数 满足
满足 ,则下列结论:
,则下列结论: 对称; ②
对称; ② 对称;
对称; ;
; 内是单调函数; ⑤方程
内是单调函数; ⑤方程 在
在 上至少有两个根。
上至少有两个根。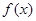 和
和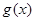 对其定义域上的任意实数x恒有:
对其定义域上的任意实数x恒有: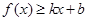 和
和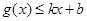 ,则称直线
,则称直线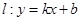 为
为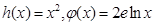 ,则可推知
,则可推知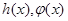 的“隔离直线”方程为 ▲
的“隔离直线”方程为 ▲  是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, 的解集为
的解集为  ,则f[f(
,则f[f( )]的值是( )
)]的值是( )