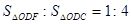题目内容
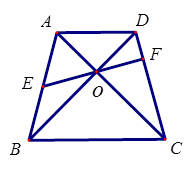
如图1,⊙O的直径AB=4,点C、D为⊙O上两点,且∠CAB=45o,F为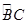 的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图2).
的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图2).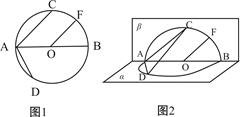
(Ⅰ)求证:OF//平面ACD;
(Ⅱ)在 上是否存在点
上是否存在点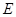 ,使得平面
,使得平面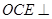 平面ACD?若存在,试指出点
平面ACD?若存在,试指出点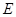 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
(1)根据线面平行的判定定理来得到证明,关键是对于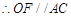 的证明。
的证明。
(2)根据题意,可以猜想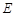 为
为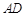 中点时满足题意,然后根据定理加以证明。
中点时满足题意,然后根据定理加以证明。
解析试题分析:.(I)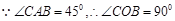
又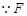 为
为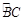 的中点,
的中点,
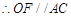 ,又
,又 平面
平面
从而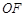 //平面
//平面 6分
6分
(II)存在,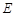 为
为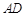 中点
中点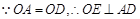
又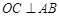 且两半圆所在平面互相垂直
且两半圆所在平面互相垂直 平面
平面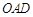
又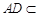 平面
平面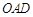
 ,由
,由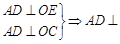 平面
平面
又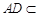 平面
平面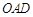
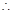 平面
平面 平面ACD 12分
平面ACD 12分
考点:线面平行和面面垂直的判定定理
点评:解决的关键是对于线面平行和面面垂直的定理的运用,属于基础题。

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
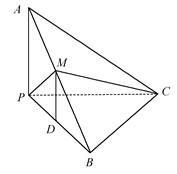
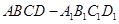 中,下底
中,下底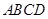 是边长为
是边长为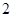 的正方形,上底
的正方形,上底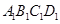 是边长为1的正方形,侧棱
是边长为1的正方形,侧棱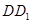 ⊥平面
⊥平面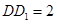 .
.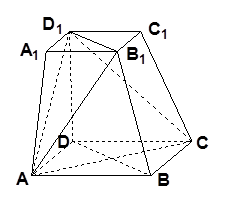
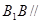 平面
平面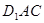 ;
;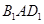 与平面
与平面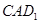 夹角的余弦值.
夹角的余弦值.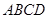 与
与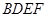 均为菱形,
均为菱形,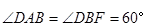 ,且
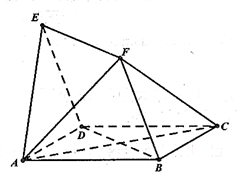
,且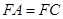 .
.
 ;
;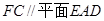 ;
;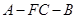 的余弦值.
的余弦值.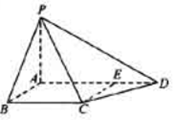
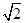 ,∠CDA=45°,求四棱锥P-ABCD的体积
,∠CDA=45°,求四棱锥P-ABCD的体积 ,如图二,在二面角
,如图二,在二面角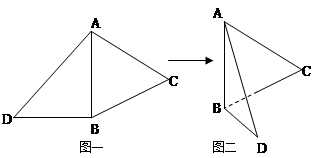
 中,
中, 底面
底面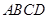 ,
,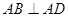 ,
,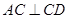 ,
,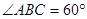 ,
,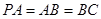 .
.
 平面
平面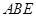 ;
;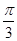 ,并说明理由.
,并说明理由.