Question

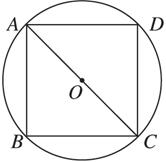
求证：在同一圆的内接矩形中，正方形的面积最大.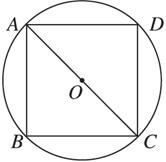

Answer 1

思维分析：如果知道圆的半径R，内接矩形的两邻边长分别为x、y，矩形面积S=xy，就是要证x=y时S最大，由矩形、圆的性质可知，矩形的对角线就是圆的直径，把x、y的关系找出来，则y可用x表示，S是关于x的函数，则可求S的最大值.?

证明：设⊙O的半径为R，矩形ABCD的两邻边长分别为x、y.?

则矩形面积S=xy（0＜x,y＜2R）.?

∵∠ABC=∠ADC=90°,?

∴A、O、C共线.∴AC=2R.?

∴x²+y²=（2R）²,?

y=（∵y＞0）.?

∴S=x.

令S′=+x·==0.

∴4R²-2x²=0.?

解得x₁=-R（舍去），x₂=R,

∴y==R=x.

又∵当x或y接近于0时，S接近于0；当x或y接近于2R时，S接近于0;?

∴当x=y=R时,S_max=2R².

∴矩形为正方形.

∴同一圆的内接矩形中，正方形面积最大.

温馨提示

在求函数最值问题时，导数是有力的工具之一.