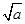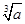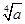题目内容
已知正数a,b,c成等差数列,且公差d≠0,求证: 不可能是等差数列。
不可能是等差数列。
 不可能是等差数列。
不可能是等差数列。 证明:由a,b,c成等差数列,不妨设b=a+d,c=a+2d,
则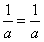 ,
,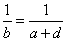 ,
,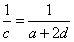 ,
,
假设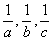 能构成等差数列,则
能构成等差数列,则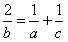 ,
,
即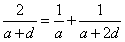 ,
,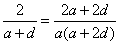 ,
,
∴2a(a+2d)=(a+d)(2a+2d),2a(a+2d)=2(a+d)2,
∴a(a+2d)=(a+d)2,a2+2ad=a2+2ad+d2,
即d2=0,d=0,这与已知d≠0矛盾,
所以假设不成立,即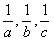 不能构成等差数列。
不能构成等差数列。
则
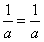 ,
,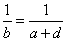 ,
,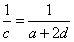 ,
,假设
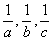 能构成等差数列,则
能构成等差数列,则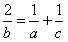 ,
,即
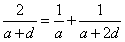 ,
,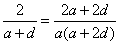 ,
,∴2a(a+2d)=(a+d)(2a+2d),2a(a+2d)=2(a+d)2,
∴a(a+2d)=(a+d)2,a2+2ad=a2+2ad+d2,
即d2=0,d=0,这与已知d≠0矛盾,
所以假设不成立,即
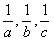 不能构成等差数列。
不能构成等差数列。
练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
已知正数a、b、c成等比数列,则下列三数也成等比数列的是( )
| A、lga lgb lgc | ||||||||
| B、10a10b10c | ||||||||
| C、5lga5lgb5lgc | ||||||||
D、
|
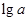
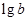
 B.
B.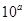

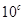 C.
C.
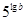
 D.
D.