题目内容
设数列{an}满足a1=2,an+1=an+3•2n-1.(1)求数列{an}的通项公式an;
(2)令bn=nan,求数列{bn}的前n项和Sn;
(3)令cn=log2
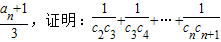 <1(n≥2).
<1(n≥2).
【答案】分析:(1)累加法:注意验证n=1的情形;
(2)表示出bn,然后利用分组求和得,Sn=3[(1•2+2•21+3•22+…+n•2n-1)-(1+2+3+…+n)],令x=1•2+2•21+3•22+…+n•2n-1,运用错位相减法可得x,代入Sn即可;
(3)由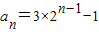 可得cn,利用裂项相消法可化简
可得cn,利用裂项相消法可化简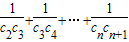 ,由其结果可得证;
,由其结果可得证;
解答:解:(1)∵a1=2,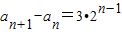 ,
,
∴an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)
=2+3×2+3×21+3×22+…+3×2n-2
=2+3(2+21+22+…+2n-2)
=2+3×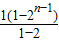 =3×2n-1-1(n≥2),
=3×2n-1-1(n≥2),
经验证n=1也成立,∴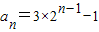 ;
;
(2)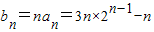 ,
,
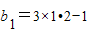 ,
,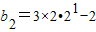 ,
,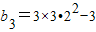 ,…,
,…,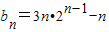 ,
,
∴Sn=3[(1•2+2•21+3•22+…+n•2n-1)-(1+2+3+…+n)],
设x=1•2+2•21+3•22+…+n•2n-1①,则2x=1•21+2•22+3•23+…+n•2n②,
①-②得,-x=1+21+22+23+…+2n-1-n•2n
=1+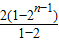 -n•2n=-1+(1-n)•2n,
-n•2n=-1+(1-n)•2n,
∴x=(n-1)2n+1,
∴Sn=3[(n-1)2n+1-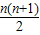 ],
],
∴Sn=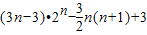 ;
;
(3)∵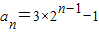 ;
;
∴cn=log22n-1=n-1,
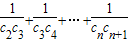 =
=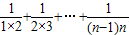
=1-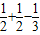 +…
+…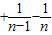 =1-
=1-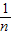 <1.
<1.
点评:本题考查由递推式求数列通项、错位相减法、裂项相消法对数列求和,考查学生的运算求解能力,综合性较强,难度较大.
(2)表示出bn,然后利用分组求和得,Sn=3[(1•2+2•21+3•22+…+n•2n-1)-(1+2+3+…+n)],令x=1•2+2•21+3•22+…+n•2n-1,运用错位相减法可得x,代入Sn即可;
(3)由
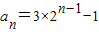 可得cn,利用裂项相消法可化简
可得cn,利用裂项相消法可化简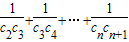 ,由其结果可得证;
,由其结果可得证;解答:解:(1)∵a1=2,
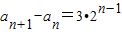 ,
,∴an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)
=2+3×2+3×21+3×22+…+3×2n-2
=2+3(2+21+22+…+2n-2)
=2+3×
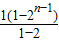 =3×2n-1-1(n≥2),
=3×2n-1-1(n≥2),经验证n=1也成立,∴
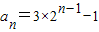 ;
;(2)
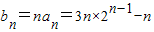 ,
,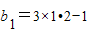 ,
,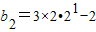 ,
,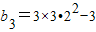 ,…,
,…,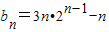 ,
,∴Sn=3[(1•2+2•21+3•22+…+n•2n-1)-(1+2+3+…+n)],
设x=1•2+2•21+3•22+…+n•2n-1①,则2x=1•21+2•22+3•23+…+n•2n②,
①-②得,-x=1+21+22+23+…+2n-1-n•2n
=1+
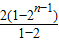 -n•2n=-1+(1-n)•2n,
-n•2n=-1+(1-n)•2n,∴x=(n-1)2n+1,
∴Sn=3[(n-1)2n+1-
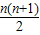 ],
],∴Sn=
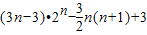 ;
;(3)∵
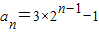 ;
;∴cn=log22n-1=n-1,
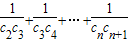 =
=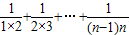
=1-
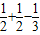 +…
+…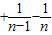 =1-
=1-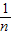 <1.
<1.点评:本题考查由递推式求数列通项、错位相减法、裂项相消法对数列求和,考查学生的运算求解能力,综合性较强,难度较大.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
设数列{an}满足a1=1,a2+a4=6,且对任意n∈N*,函数f(x)=(an-an+1+an+2)x+an+1?cosx-an+2sinx满足f′(
)=0若cn=an+
,则数列{cn}的前n项和Sn为( )
| π |
| 2 |
| 1 |
| 2an |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|