题目内容
省少年篮球队要从甲、乙两所体校选拔队员。现将这两所体校共20名学生的身高绘制成如下茎叶图(单位:cm):若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“非高个子”.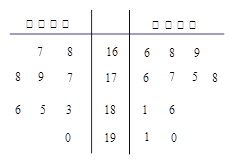
(1)用分层抽样的方法从“高个子”和“非高个子”中抽取5人,如果从这5人中随
机选2人,那么至少有一人是“高个子”的概率是多少?
(2)从两队的“高个子”中各随机抽取1人,求恰有1人身高达到190cm的概率.
(Ⅰ) ;(Ⅱ)
;(Ⅱ)
解析试题分析:(Ⅰ)根据茎叶图可知这20名学生中有“高个子”8人,“非高个子”12人,因为采用分层抽样的方法从中抽取5人,故抽取比例为 .根据这个比例可以求“高个子”和“非高个子”所抽取的人数.然后用古典概型公式可求出所要求的概率.
.根据这个比例可以求“高个子”和“非高个子”所抽取的人数.然后用古典概型公式可求出所要求的概率.
(Ⅱ)根据茎叶图可知,两队的“高个子”各有4人,其中甲队身高达到190cm的有1人,乙队身高达到190cm的有2人.
一一列举出从两队中各取1人的所有可能结果 ,数出其中恰有一人达到190cm的所有可能结果
,数出其中恰有一人达到190cm的所有可能结果 .
.
由古典概型公式 得所求概率.
得所求概率.
试题解析:(Ⅰ)根据茎叶图可知这20名学生中有“高个子”8人,“非高个子”12人,用分层抽样的方法从中抽取5人,则应从“高个子”中抽取 人,从“非高个子”中抽取
人,从“非高个子”中抽取 人。
人。
用 表示“至少有一名‘高个子’被选中”,则它的对立事件
表示“至少有一名‘高个子’被选中”,则它的对立事件 表示“没有一名‘高个子’被选中”,所以
表示“没有一名‘高个子’被选中”,所以 .
.
(Ⅱ)根据茎叶图可知,两队的“高个子”各有4人,依次设为:甲1、甲2、甲3、甲4,乙1、乙2、乙3、乙4. 其中甲4、乙3、乙4身高达到190cm.
从两队中各取1人,则共有以下16种可能结果:甲1乙1、甲1乙2、甲1乙3、甲1乙4、甲2乙1、甲2乙2、甲2乙3、甲2乙4、甲3乙1、甲3乙2、甲3乙3、甲3乙4、甲4乙1、甲4乙2、甲4乙3、甲4乙4.其中恰有一人达到190cm的有以下8种可能结果:甲1乙3、甲1乙4、甲2乙3、甲2乙4、甲3乙3、甲3乙4、甲4乙1、甲4乙2.
所以从两队的“高个子”中各随机抽取1人,恰有1人身高达到190cm的概率为:
考点:1、茎叶图;2、古典概型.

在某校高三学生的数学校本课程选课过程中,规定每位同学只能选一个科目.已知某班第一小组与第二小组各有六位同学选择科目甲或科目乙,情况如下表:
| | 科目甲 | 科目乙 | 总计 |
| 第一小组 | 1 | 5 | 6 |
| 第二小组 | 2 | 4 | 6 |
| 总计 | 3 | 9 | 12 |
(1)求选出的4人均选科目乙的概率;
(2)设
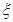 为选出的4个人中选科目甲的人数,求
为选出的4个人中选科目甲的人数,求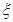 的分布列和数学期望.
的分布列和数学期望. 气象部门提供了某地今年六月份(30天)的日最高气温的统计表如下:
| 日最高气温t (单位:℃) | t 22℃ 22℃ | 22℃< t 28℃ 28℃ | 28℃< t  32℃ 32℃ | 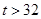 ℃ ℃ |
| 天数 | 6 | 12 |  |  |
 和
和 数据不清楚,但气象部门提供的资料显示,六月份的日最高气温不高于32℃的频率为0.9.
数据不清楚,但气象部门提供的资料显示,六月份的日最高气温不高于32℃的频率为0.9.(Ⅰ) 若把频率看作概率,求
 ,
, 的值;
的值;(Ⅱ) 把日最高气温高于32℃称为本地区的 “高温天气”,根据已知条件完成下面
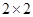 列联表,并据此你是否有95%的把握认为本地区的“高温天气”与西瓜“旺销”有关?说明理由.
列联表,并据此你是否有95%的把握认为本地区的“高温天气”与西瓜“旺销”有关?说明理由.| | 高温天气 | 非高温天气 | 合计 |
| 旺销 | 1 | | |
| 不旺销 | | 6 | |
| 合计 | | | |

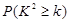 | 0.10 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
某品牌的汽车4S店,对最近100位采用分期付款的购车者进行统计,统计结果如下表所示:
| 付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频数 | 40 | 20 | 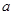 | 10 | 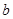 |
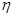 表示经销一辆汽车的利润.
表示经销一辆汽车的利润.(1)求上表中
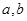 的值;
的值;(2)若以频率作为概率,求事件
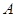 :“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的概率
:“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的概率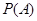 ;(3)求
;(3)求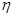 的分布列及数学期望
的分布列及数学期望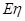 .
. 某市 、
、 、
、 、
、 四所中学报名参加某高校今年自主招生的学生人数如下表所示:
四所中学报名参加某高校今年自主招生的学生人数如下表所示:
| 中学 |  |  |  |  |
| 人数 |  |  |  |  |
 名参加问卷调查.
名参加问卷调查.(1)问
 、
、 、
、 、
、 四所中学各抽取多少名学生?
四所中学各抽取多少名学生?(2)从参加问卷调查的
 名学生中随机抽取两名学生,求这两名学生来自同一所中学的概率;
名学生中随机抽取两名学生,求这两名学生来自同一所中学的概率;(3)在参加问卷调查的
 名学生中,从来自
名学生中,从来自 、
、 两所中学的学生当中随机抽取两名学生,用
两所中学的学生当中随机抽取两名学生,用 表示抽得
表示抽得 中学的学生人数,求
中学的学生人数,求 的分布列.
的分布列. 在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:1,2,3,4,5
| 编号n | 1 | 2 | 3 | 4 | 5 |
| 成绩xn | 70 | 76 | 72 | 70 | 72 |
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
(注:方差s2=
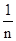 [(x1-
[(x1- )2+(x2-
)2+(x2- )2+…+(xn-
)2+…+(xn- )2],其中
)2],其中 为x1,x2,…,xn的平均数)
为x1,x2,…,xn的平均数) 某经销商试销A、B两种商品一个月(30天)的记录如下:
| 日销售量(件) | 0 | 1 | 2 | 3 | 4 | 5 |
| 商品A的频数 | 2 | 5 | 7 | 7 | 5 | 4 |
| 商品B的频数 | 4 | 4 | 6 | 8 | 5 | 3 |
(Ⅰ)求B商品日销售量不超过3件的概率;
(Ⅱ)由于某种原因,该商家决定只选择经销A、B商品的一种,你认为应选择哪种商品,说明理由。
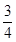 ,
,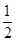 ,
,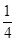 .
. 、
、 ,记
,记 .
. 取最大值的概率;
取最大值的概率;