题目内容
(2013•南充三模)已知函数f(x)=cos(x-
)-mcosx(m∈R)的图象过p(0,-
),且△ABC内角A、B、C所对应边分别为a、b、c,若f(B)=-
,a=2
,c=
(I)求m的值及f(x)的单调递增区间
(II)求△ABC的面积.
| 2π |
| 3 |
| 3 |
| 2 |
| ||
| 2 |
| 6 |
| 3 |
(I)求m的值及f(x)的单调递增区间
(II)求△ABC的面积.
分析:(I)由f(0)=-
可求得m=1;从而可求得f(x)=
sin(x-
),利用正弦函数的单调性即可求得f(x)的单调递增区间;
(II)在△ABC中,由f(B)=-
可求得B,从而利用S△ABC=
acsinB即可求得答案.
| 3 |
| 2 |
| 3 |
| π |
| 3 |
(II)在△ABC中,由f(B)=-
| ||
| 2 |
| 1 |
| 2 |
解答:解:(I)∵f(0)=cos(-
)-m=-
∴m=1…(2分)
∴f(x)=cos(x-
)-cosx=-
cosx+
sinx-cosx
=
sinx-
cosx
=
sin(x-
) …(4分)
∴2kπ-
≤x-
≤2kπ+
(k∈Z),
∴2kπ-
≤x≤2kπ+
(k∈Z),…(6分)
∴f(x)的单调递增区间为[2kπ-
,2kπ+
](k∈Z) …(7分)
(Ⅱ)f(B)=
sin(B-
)=-
,
∴sin(B-
)=-
,
∵0<B<π,
∴-
<B-
<
,
∴B-
=-
,
∴B=
…(10分)
则S△ABC=
acsinB=
×2
×
×
=
,
∴△ABC的面积为
…(12分)
| 2π |
| 3 |
| 3 |
| 2 |
∴m=1…(2分)
∴f(x)=cos(x-
| 2π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
=
| ||
| 2 |
| 3 |
| 2 |
=
| 3 |
| π |
| 3 |
∴2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
∴2kπ-
| π |
| 6 |
| 5π |
| 6 |
∴f(x)的单调递增区间为[2kπ-
| π |
| 6 |
| 5π |
| 6 |
(Ⅱ)f(B)=
| 3 |
| π |
| 3 |
| ||
| 2 |
∴sin(B-
| π |
| 3 |
| 1 |
| 2 |
∵0<B<π,
∴-
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∴B-
| π |
| 3 |
| π |
| 6 |
∴B=
| π |
| 6 |
则S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 6 |
| 3 |
| 1 |
| 2 |
3
| ||
| 2 |
∴△ABC的面积为
3
| ||
| 2 |
点评:本题考查三角函数间恒等变换,考查正弦函数的单调性与三角形的面积,考查推理与运算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013•南充三模)M公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在180分以上者到“甲部门”工作;180分以下者到“乙部门”工作.
(2013•南充三模)M公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在180分以上者到“甲部门”工作;180分以下者到“乙部门”工作.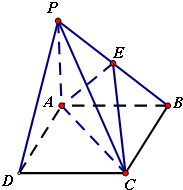 (2013•南充三模)如图,在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,PA⊥平面ABCD,E为PB中点,PB=4
(2013•南充三模)如图,在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,PA⊥平面ABCD,E为PB中点,PB=4 (2013•南充三模)如图是一个空间几何体的三视图,这个几何体的体积是( )
(2013•南充三模)如图是一个空间几何体的三视图,这个几何体的体积是( )