题目内容
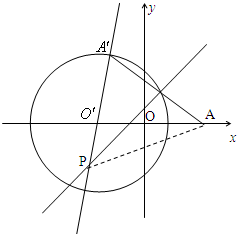 如图,已知圆O′:(x+2)2+y2=8及点A(2,0),在圆O'上任取一点A′,连AA′并作AA′的中垂线l,设l与直线O′A′交于点P,若点A′取遍圆O′上的点.
如图,已知圆O′:(x+2)2+y2=8及点A(2,0),在圆O'上任取一点A′,连AA′并作AA′的中垂线l,设l与直线O′A′交于点P,若点A′取遍圆O′上的点.(Ⅰ)求点P的轨迹C的方程;
(Ⅱ)若过点O′的直线m与曲线C交于M、N两点,且|AM|=|AN|,求直线m的方程.
分析:(Ⅰ)利用l是线段AA′的中垂线,可得点P的轨迹是双曲线,从而可求轨迹C的方程;
(Ⅱ)设直线m的方程代入双曲线方程,求出MN中点坐标,利用|AM|=|AN|,可得斜率互为负倒数,从而可得直线的向量,进而可求直线m的方程.
(Ⅱ)设直线m的方程代入双曲线方程,求出MN中点坐标,利用|AM|=|AN|,可得斜率互为负倒数,从而可得直线的向量,进而可求直线m的方程.
解答:解:(Ⅰ)∵l是线段AA′的中垂线,∴|PA|=|PA′|,
∴||PA|-|PO′||=||PA′|-|PO′||=|O′A′|=2
.
即点P在以O′、A为焦点,以4为焦距,以2
为实轴长的双曲线上,
故轨迹C的方程为
-
=1.
(Ⅱ)设M(x1,y1),N(x2,y2),直线m的方程为y=k(x+2),代入双曲线方程,可得(1-k2)x2-4k2x-2k2-2=0
∴x1+x2=
,∴y1+y2=
,
∴MN中点坐标为(
,
)
∵|AM|=|AN|,∴
×k=-1
∴k2=
,∴k=±
∴直线m的方程为y=±
(x+2).
∴||PA|-|PO′||=||PA′|-|PO′||=|O′A′|=2
| 2 |
即点P在以O′、A为焦点,以4为焦距,以2
| 2 |
故轨迹C的方程为
| x2 |
| 2 |
| y2 |
| 2 |
(Ⅱ)设M(x1,y1),N(x2,y2),直线m的方程为y=k(x+2),代入双曲线方程,可得(1-k2)x2-4k2x-2k2-2=0
∴x1+x2=
| 4k2 |
| 1-k2 |
| 4k |
| 1-k2 |
∴MN中点坐标为(
| 2k2 |
| 1-k2 |
| 2k |
| 1-k2 |
∵|AM|=|AN|,∴
| ||
|
∴k2=
| 1 |
| 3 |
| ||
| 3 |
∴直线m的方程为y=±
| ||
| 3 |
点评:本题考查双曲线的定义,考查双曲线的标准方程,考查直线与双曲线的位置关系,考查韦达定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 如图,已知圆O:x2+y2=1,O为坐标原点.
如图,已知圆O:x2+y2=1,O为坐标原点.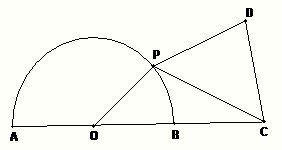 如图:已知圆O的直径是2,点C在直径AB的延长线上,BC=1,点P是圆O上的一个动点,以PC为边作正三角形PCD,且点D与圆心分别在PC的两侧,求四边形OPDC面积的最大值.
如图:已知圆O的直径是2,点C在直径AB的延长线上,BC=1,点P是圆O上的一个动点,以PC为边作正三角形PCD,且点D与圆心分别在PC的两侧,求四边形OPDC面积的最大值. 如图,已知圆O:x2+y2=2交x轴于A,B两点,点P(-1,1)为圆O上一点.曲线C是以AB为长轴,离心率为
如图,已知圆O:x2+y2=2交x轴于A,B两点,点P(-1,1)为圆O上一点.曲线C是以AB为长轴,离心率为 如图,已知圆O的直径AB=4,定直线L到圆心的距离为4,且直线L垂直直线AB.点P是圆O上异于A、B的任意一点,直线PA、PB分别交L与M、N点.
如图,已知圆O的直径AB=4,定直线L到圆心的距离为4,且直线L垂直直线AB.点P是圆O上异于A、B的任意一点,直线PA、PB分别交L与M、N点. 如图,已知圆O外有一点P,作圆O的切线PM,M为切点,过PM的中点N,作割线NAB,交圆于A、B两点,连接PA并延长,交圆O于点C,连续PB交圆O于点D,若MC=BC.
如图,已知圆O外有一点P,作圆O的切线PM,M为切点,过PM的中点N,作割线NAB,交圆于A、B两点,连接PA并延长,交圆O于点C,连续PB交圆O于点D,若MC=BC.