题目内容
已知![]() .
.
(1)写出符合题意的一个函数![]() ;
;
(2)若![]() (一1)=0,求
(一1)=0,求![]() 在[一2,2]上的最大值和最小值;
在[一2,2]上的最大值和最小值;
(3)若函数g(![]() )=
)=![]() 分别在(一∞,一2]和[2,+∞)上均为增函数,求
分别在(一∞,一2]和[2,+∞)上均为增函数,求![]() 的取值范围.
的取值范围.
解:(1)∵![]() ,其中
,其中![]() 为任意常数,
为任意常数,
∴![]()
注:![]() 取任意一个值都是正确答案.
取任意一个值都是正确答案.
(2)由![]() ,得
,得![]() =4.∴
=4.∴![]() .由
.由![]() 得
得![]() 或
或![]() .
.
又![]() ,
,![]() ,
,![]() ,
,
![]() (2)=6.∴
(2)=6.∴![]() 在[一2,2]上的最大值为6,最小值为一l4.
在[一2,2]上的最大值为6,最小值为一l4.
(3)∵g(![]() )=
)=![]() 3-
3-![]()
![]() 2-4
2-4![]() +1,∴g’(
+1,∴g’(![]() )=3
)=3![]() 2―2
2―2![]()
![]() -4.
-4.
g’(![]() )的图像是开口向上且过点(0,-4)的抛物线.
)的图像是开口向上且过点(0,-4)的抛物线.
故由题设可知g’(-2)≥0,g’(2)≥0,
即![]()
∴-2![]() ,∴
,∴![]() 的取值范围为[一2,2].
的取值范围为[一2,2].

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
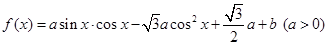
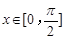 ,
, 的最小值是
的最小值是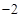 ,最大值是
,最大值是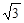 ,求实数
,求实数 的值.
的值.
 ,
, 的最小值是
的最小值是 ,最大值是
,最大值是 ,求实数
,求实数 的值
的值 