题目内容
设u、v是实数,则(u-v)2+(| 4-u2 |
分析:从数式的形与构来看与两点间的距离公式的平方同构,可视为两点间的距离的平方即可找到解题入口.
解答:解:(u-v)2+(
-2v-5)2可视为点P(u,
)与点Q(v,2v+5 )之间的距离的平方,P的轨迹为上半圆x2+y2=4(y≥0),Q的轨迹为曲线C:y=2x+5,
圆心(0,0)到直线y=2x+5的距离为
=
,圆的半径为2,
所以(u-v)2+(
-2v-5)2的最小值为(
-2)2=9-4
.
故答案为:9-4
.
| 4-u2 |
| 4-u2 |
圆心(0,0)到直线y=2x+5的距离为
| 5 | ||
|
| 5 |
所以(u-v)2+(
| 4-u2 |
| 5 |
| 5 |
故答案为:9-4
| 5 |
点评:数式的最值问题,通常可通过对其结构与形式特征进行观察,类比,联想与已知的定理、定义、性质等形式类似,实现转化,构建解题思路.

练习册系列答案
相关题目
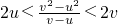 .
.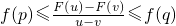 成立,则称F(x)是f(x)在区间I上的甲函数,f(x)是F(x)在区间I上的乙函数.
成立,则称F(x)是f(x)在区间I上的甲函数,f(x)是F(x)在区间I上的乙函数.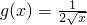 是
是 的乙函数.
的乙函数.