题目内容
已知平行六面体ABCD-A1B1C1D1中，A1A⊥平面ABCD，AB=4，AD=2．若B1D⊥BC，直线B1D与平面ABCD所成的角等于30°，求平行六面体ABCD-A1B1C1D1的体积．
分析：根据题目所给条件，可判断出几何体的高是A1A，只要求出底面面积即可，根据题意，说明BC⊥BD．容易求得底面面积．
解答：
解：连接BD，因为B1B⊥平面ABCD，
B1D⊥BC，所以BC⊥BD．
在△BCD中，BC=2，CD=
所以BD=2
．
又因为直线B1D与平面ABCD所成的角等于30°，
所以∠B1DB=30°，于是BB1=
BD=2．
故平行六面体ABCD-A1B1C1D1的体积为SABCD•BB1=8
．
解：连接BD，因为B1B⊥平面ABCD，B1D⊥BC，所以BC⊥BD．
在△BCD中，BC=2，CD=
所以BD=2
| 3 |
又因为直线B1D与平面ABCD所成的角等于30°，
所以∠B1DB=30°，于是BB1=
| 1 | ||
|
故平行六面体ABCD-A1B1C1D1的体积为SABCD•BB1=8
| 3 |
点评：本题考查棱柱的体积，考查空间想象能力，逻辑思维能力，是基础题．
练习册系列答案
名校课堂系列答案
相关题目
如图，已知平行六面体ABC-A1B1C1的底面为正方形，O1，O分别为上、下底面中心，且A1在底面ABCD上的射影为O．
如图，已知平行六面体ABCD-A1B1C1D1．
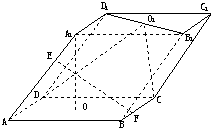如图，已知平行六面体ABC-A1B1C1的底面为正方形，O1，O分别为上、下底面中心，且A1在底面ABCD上的射影为O．
如图，已知平行六面体ABCD-A1B1C1D1．
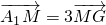，设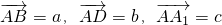
，用向量a、b、c表示向量
；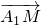