题目内容
已知数列{an}的前n项和Sn=n(n+2),数列{bn}的前n项和为Tn,且有 .
.
(1)求数列{an},{bn}的通项an,bn;
(2)设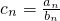 ,试判断数列{cn}的单调性,并证明你的结论.
,试判断数列{cn}的单调性,并证明你的结论.
(3)在(2)的前提下,设Mn是数列{cn}的前n项和,证明: .
.
(1)解:∵Sn=n(n+2),
∴当n≥2时,an=Sn-Sn-1=2n+1
当n=1时,a1=S1=3满足上式
∴an=2n+1
∵
∴Tn+1-Tn=2bn-1
∴bn+1=2bn-1
∴bn+1-1=2(bn-1)
∴{bn-1}是公比为2的等比数列
∴
∴
(2)解: ,数列{cn}为递减数列
,数列{cn}为递减数列
证明:∵
=
∴数列{cn}为递减数列
(3)证明:∵
∴Mn=c1+c2+…+cn≥
令 ①
①
∴ ②
②
①-②: =
=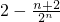
∴
∴ =
=
∴
分析:(1)根据当n≥2时,an=Sn-Sn-1,可求数列{an}的通项an,根据 ,可得bn+1=2bn-1,从而{bn-1}是公比为2的等比数列,故可求数列{bn}的通项bn;
,可得bn+1=2bn-1,从而{bn-1}是公比为2的等比数列,故可求数列{bn}的通项bn;
(2) ,数列{cn}为递减数列,再用作差法证明即可;
,数列{cn}为递减数列,再用作差法证明即可;
(3)根据 ,可得Mn=c1+c2+…+cn≥
,可得Mn=c1+c2+…+cn≥ ,利用错位相消法,求出右边的和,即可证得结论.
,利用错位相消法,求出右边的和,即可证得结论.
点评:本题以数列的和为载体,考查数列的通项,考查数列的单调性,考查不等式的证明,同时考查错位相减法求数列的和,综合性强.
∴当n≥2时,an=Sn-Sn-1=2n+1
当n=1时,a1=S1=3满足上式
∴an=2n+1
∵

∴Tn+1-Tn=2bn-1
∴bn+1=2bn-1
∴bn+1-1=2(bn-1)
∴{bn-1}是公比为2的等比数列
∴

∴

(2)解:
 ,数列{cn}为递减数列
,数列{cn}为递减数列证明:∵

=

∴数列{cn}为递减数列
(3)证明:∵

∴Mn=c1+c2+…+cn≥

令
 ①
①∴
 ②
②①-②:
 =
=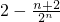
∴

∴
 =
=
∴

分析:(1)根据当n≥2时,an=Sn-Sn-1,可求数列{an}的通项an,根据
 ,可得bn+1=2bn-1,从而{bn-1}是公比为2的等比数列,故可求数列{bn}的通项bn;
,可得bn+1=2bn-1,从而{bn-1}是公比为2的等比数列,故可求数列{bn}的通项bn;(2)
 ,数列{cn}为递减数列,再用作差法证明即可;
,数列{cn}为递减数列,再用作差法证明即可;(3)根据
 ,可得Mn=c1+c2+…+cn≥
,可得Mn=c1+c2+…+cn≥ ,利用错位相消法,求出右边的和,即可证得结论.
,利用错位相消法,求出右边的和,即可证得结论.点评:本题以数列的和为载体,考查数列的通项,考查数列的单调性,考查不等式的证明,同时考查错位相减法求数列的和,综合性强.

练习册系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |