题目内容
已知等比数列{an}的各项均为正数,且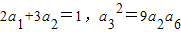 .
.(I)求{an}的通项公式.
(II)令cn=-log3an,求数列{cnan}的前n项和Sn.
【答案】分析:(I)由已知中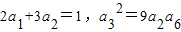 .设等比数列公比为q,构造方程组,解得数列的首项和公比,代入等比数列通项公式,可得{an}的通项公式.
.设等比数列公比为q,构造方程组,解得数列的首项和公比,代入等比数列通项公式,可得{an}的通项公式.
(II)由(I)中{an}的通项公式及cn=-log3an,求出数列数列{cn}的通项公式,进而求出数列{cnan}的通项公式,利用错位相减法,可得答案.
解答:解:(I)设等比数列公比为q,由题意,
解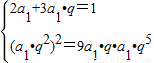 得
得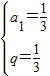 …(4分)
…(4分)
故{an}的通项公式为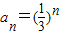 …(6分)
…(6分)
(II)由(I)得:cn=-log3an=n,
∴{cnan}=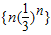 …(7分)
…(7分)
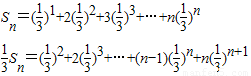
相减得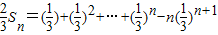 …(9分)
…(9分)
=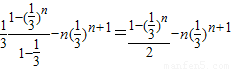
∴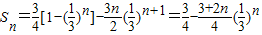 …(12分)
…(12分)
点评:本题考查的知识点是等比数列的通项公式,数列求和,(I)的关键是构造方程组,求出首项和公比,(II)的关键是根据通项是等差数列与等比数列相乘的形式,而选用错位相减法.
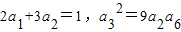 .设等比数列公比为q,构造方程组,解得数列的首项和公比,代入等比数列通项公式,可得{an}的通项公式.
.设等比数列公比为q,构造方程组,解得数列的首项和公比,代入等比数列通项公式,可得{an}的通项公式.(II)由(I)中{an}的通项公式及cn=-log3an,求出数列数列{cn}的通项公式,进而求出数列{cnan}的通项公式,利用错位相减法,可得答案.
解答:解:(I)设等比数列公比为q,由题意,
解
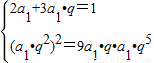 得
得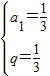 …(4分)
…(4分)故{an}的通项公式为
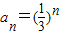 …(6分)
…(6分)(II)由(I)得:cn=-log3an=n,
∴{cnan}=
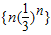 …(7分)
…(7分)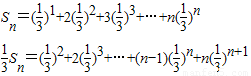
相减得
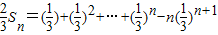 …(9分)
…(9分)=
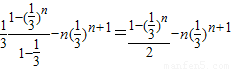
∴
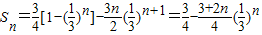 …(12分)
…(12分)点评:本题考查的知识点是等比数列的通项公式,数列求和,(I)的关键是构造方程组,求出首项和公比,(II)的关键是根据通项是等差数列与等比数列相乘的形式,而选用错位相减法.

练习册系列答案
相关题目