题目内容
设偶函数f(x)的定义域为R,当x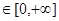 时f(x)是增函数,则f(-2),f(
时f(x)是增函数,则f(-2),f(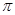 ),f(-3)的大小关系是( )
),f(-3)的大小关系是( )
A.f(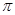 )>f(-3)>f(-2)
B.f(
)>f(-3)>f(-2)
B.f(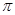 )>f(-2)>f(-3)
)>f(-2)>f(-3)
C.f(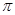 )<f(-3)<f(-2)
D.f(
)<f(-3)<f(-2)
D.f(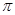 )<f(-2)<f(-3)
)<f(-2)<f(-3)
【答案】
A
【解析】
试题分析:∵偶函数f(x)的定义域为R,当x 时f(x)是增函数,则可知在区间(-∞,0]上f(x)是单调递减函数,∴f(-π)=f(π),∴f(π)>f(-3)>f(-2),故选A.
时f(x)是增函数,则可知在区间(-∞,0]上f(x)是单调递减函数,∴f(-π)=f(π),∴f(π)>f(-3)>f(-2),故选A.
考点:本试题主要考查了函数的奇偶性和单调性的综合运用。是中等试题。
点评:解决该试题的关键是能利用对称性,将已知的变量变换到一个对应的单调区间,然后利用已知的区间的单调性,结合变量的大小关系得到结论。

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
设
f(x)是连续函数,且为偶函数,在对称区间[-a,a]上的积分 ,由定积分的几何意义和性质得
,由定积分的几何意义和性质得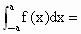
[
]|
A .0 |
B . |
|
C . |
D . |