题目内容
2.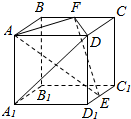 如图所示,在正方体ABCD-A1B1C1D1中,E为棱C1D1的中点,F为棱BC的中点.求证:直线AE⊥直线DA1.
如图所示,在正方体ABCD-A1B1C1D1中,E为棱C1D1的中点,F为棱BC的中点.求证:直线AE⊥直线DA1.
分析 连接AD1,BC1,利用DA1⊥AD1,DA1⊥AB,又AB∩AD1=A,说明DA1⊥面ABC1D1,然后证明DA1⊥AE.
解答  证明:连接AD1,BC1,由正方体的性质可知 DA1⊥AD1,DA1⊥AB,
证明:连接AD1,BC1,由正方体的性质可知 DA1⊥AD1,DA1⊥AB,
又AB∩AD1=A,
∴DA1⊥面ABC1D1,
又AE?面ABC1D1,
∴DA1⊥AE.
点评 本题考查直线与平面垂直的性质的应用,考查逻辑推理能力,空间想象能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.设f(x)是定义在R上的奇函数,f(2)=0,当x>0时,有$\frac{xf′(x)-f(x)}{{x}^{2}}$<0恒成立,则$\frac{f(x)}{x}>0$的解集为( )
| A. | (-2,0)∪(2,+∞) | B. | (-2,0)∪(0,2) | C. | (-∞,-2)∪(2,+∞) | D. | (-∞,-2)∪(0,2) |
17.已知M(-2,0),N(2,0),|PM|-|PN|=3,则动点P的轨迹是( )
| A. | 双曲线 | B. | 双曲线左边一支 | C. | 双曲线右边一支 | D. | 一条射线 |
14.已知函数f(x)=ex-2x-1的两个零点为0,x1,则x1所在的区间是( )
| A. | (-2,-1) | B. | (-1,0) | C. | (0,1) | D. | (1,2) |
 如图,A,B是单位圆上的相异两定点(O为圆心),且∠AOB=θ(θ为锐角).点C为单位圆上的动点,线段AC交线段OB于点M.
如图,A,B是单位圆上的相异两定点(O为圆心),且∠AOB=θ(θ为锐角).点C为单位圆上的动点,线段AC交线段OB于点M.