题目内容
已知O为坐标原点,直线y=x+a与圆x2+y2=4分别交于A,B两点.若
?
=-2,则实数a的值为( )
| OA |
| OB |
| A、1 | ||
B、
| ||
| C、±1 | ||
D、±
|
分析:设A(x1,y1),B(x2,y2).把直线与圆的方程联立化为2x2+2ax+a2-4=0,由于直线与圆相交于两点,可得△>0.得到根与系数的关系,再利用数量积运算即可得出.
解答:解:设A(x1,y1),B(x2,y2).
联立
,化为2x2+2ax+a2-4=0,
∵直线与圆相交于两点,
∴△=4a2-8(a2-4)>0,化为a2<8.(*)
∴x1+x2=-a,x1x2=
.
∵
•
=-2,
∴x1x2+y1y2=-2,
∵y1y2=(x1+a)(x2+a)=x1x2+a(x1+x2)+a2,代入上式可得2x1x2+a(x1+x2)+a2=-2.
∴2×
+a×(-a)+a2=-2.
化为a2=2满足(*)
解得a=±
.
故选:D.
联立
|
∵直线与圆相交于两点,
∴△=4a2-8(a2-4)>0,化为a2<8.(*)
∴x1+x2=-a,x1x2=
| a2-4 |
| 2 |
∵
| OA |
| OB |
∴x1x2+y1y2=-2,
∵y1y2=(x1+a)(x2+a)=x1x2+a(x1+x2)+a2,代入上式可得2x1x2+a(x1+x2)+a2=-2.
∴2×
| a2-4 |
| 2 |
化为a2=2满足(*)
解得a=±
| 2 |
故选:D.
点评:本题考查了直线与圆相交问题转化为方程联立得到根与系数的关系、数量积运算等基础知识与基本技能方法,属于中档题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
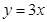 ,边AB所在的直
,边AB所在的直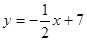 ,且顶点B的横坐标为6。
,且顶点B的横坐标为6。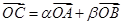 ,其中
,其中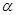
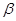 ∈R且
∈R且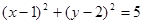 B.3x+2y-11=0 C.2x-y=0 D.x+2y=5
B.3x+2y-11=0 C.2x-y=0 D.x+2y=5