题目内容
我们知道，在边长为2a的正三角形内任一点到三边的距离之和为定值| 3 |
分析：由平面图形中点的性质类比推理出空间里的线的性质，由平面图形中线的性质类比推理出空间中面的性质，由平面图形中面的性质类比推理出空间中体的性质．或是由二维类比推理到三维，故由在边长为2a的正三角形内任一点到三边的距离之和为定值
a（二维与线有关性质）推断出在边长为3a的正四面体内任一点到其四个面的距离之和为定值（三维与面有关的性质）
| 3 |
解答：解：在由平面图形的性质向空间物体的性质进行类比时，常用的思路有：
由平面图形中点的性质类比推理出空间里的线的性质，
由平面图形中线的性质类比推理出空间中面的性质，
由平面图形中面的性质类比推理出空间中体的性质．
或是由二维类比推理到三维，
故由在边长为2a的正三角形内任一点到三边的距离之和为定值
a（二维与线有关性质）
推断出在边长为3a的正四面体内任一点到其四个面的距离之和为定值
a
故答案为：
a
由平面图形中点的性质类比推理出空间里的线的性质，
由平面图形中线的性质类比推理出空间中面的性质，
由平面图形中面的性质类比推理出空间中体的性质．
或是由二维类比推理到三维，
故由在边长为2a的正三角形内任一点到三边的距离之和为定值
| 3 |
推断出在边长为3a的正四面体内任一点到其四个面的距离之和为定值
| 6 |
故答案为：
| 6 |
点评：类比推理的一般步骤是：（1）找出两类事物之间的相似性或一致性；（2）用一类事物的性质去推测另一类事物的性质，得出一个明确的命题（猜想）．
练习册系列答案
相关题目
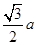，类比上述结论，在边长为a的正四面体内任一点到其四个面的距离之和为定值 。
，类比上述结论，在棱长为a的正四面体内任一点到其四个面的距离之和为定值 ．
，类比上述结论，在边长为3a的正四面体内任一点到其四个面的距离之和为定值 ．