题目内容
已知函数f(x)=ln(ax+1)+ ,x≥0,其中a>0,
,x≥0,其中a>0,
(Ⅰ)若f(x)在x=1处取得极值,求a的值;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)若f(x)的最小值为1,求a的取值范围。
 ,x≥0,其中a>0,
,x≥0,其中a>0,(Ⅰ)若f(x)在x=1处取得极值,求a的值;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)若f(x)的最小值为1,求a的取值范围。
(Ⅰ)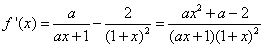 ,
,
∵f(x)在x=1处取得极值,
∴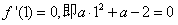 ,
,
解得a=1;
(Ⅱ)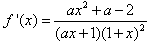 ,
,
∵x≥0,a>0,
∴ax+1>0,
①当a≥2时,在区间(0,+∞)上,f′(x)>0,∴f(x)的单调增区间为(0,+∞);
②当0<a<2时,由f′(x)>0解得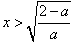 ,
,
由f′(x)<0,解得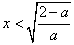 ,
,
∴f(x)的单调减区间为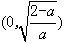 ,单调增区间为
,单调增区间为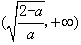 ;
;
(Ⅲ)当a≥2时,由(Ⅱ)①知,f(x)的最小值为f(0)=1;
当0<a<2时,由(Ⅱ)②知,
f(x)在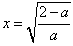 处取得最小值
处取得最小值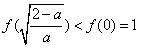 ;
;
综上可知,若f(x)的最小值为1,则a的取值范围是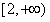 。
。
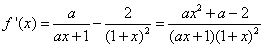 ,
, ∵f(x)在x=1处取得极值,
∴
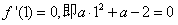 ,
,解得a=1;
(Ⅱ)
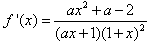 ,
,∵x≥0,a>0,
∴ax+1>0,
①当a≥2时,在区间(0,+∞)上,f′(x)>0,∴f(x)的单调增区间为(0,+∞);
②当0<a<2时,由f′(x)>0解得
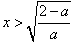 ,
,由f′(x)<0,解得
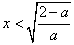 ,
,∴f(x)的单调减区间为
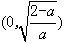 ,单调增区间为
,单调增区间为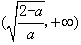 ;
;(Ⅲ)当a≥2时,由(Ⅱ)①知,f(x)的最小值为f(0)=1;
当0<a<2时,由(Ⅱ)②知,
f(x)在
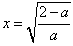 处取得最小值
处取得最小值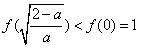 ;
;综上可知,若f(x)的最小值为1,则a的取值范围是
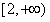 。
。 
练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目