题目内容
在△ABC中,角A,B,C所对的边分别为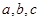 ,已知函数
,已知函数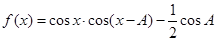
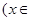 R).
R).
(Ⅰ)求函数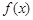 的最小正周期和最大值;
的最小正周期和最大值;
(Ⅱ)若函数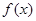 在
在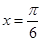 处取得最大值,且
处取得最大值,且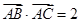 ,求
,求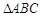 的面积
的面积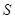 .
.
【答案】
(Ⅰ)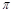 ,
,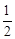 ;(Ⅱ)
;(Ⅱ)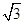 .
.
【解析】
试题分析:(Ⅰ)利用三角函数公式把函数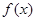 化简为一个角的三角函数,从而易得函数
化简为一个角的三角函数,从而易得函数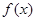 的最小正周期和最大值;(Ⅱ)由(Ⅰ)函数先求角A,再由向量数量积公式求
的最小正周期和最大值;(Ⅱ)由(Ⅰ)函数先求角A,再由向量数量积公式求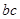 的值,从而利用
的值,从而利用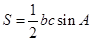 求得三角形面积.
求得三角形面积.
试题解析:(Ⅰ)依题意,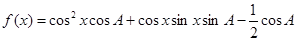 2分
2分
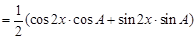
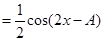 5分
5分
所以函数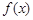 的最小正周期是
的最小正周期是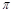 ,
,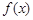 有最大值
有最大值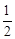 .
7分
.
7分
(Ⅱ)由(I)知:由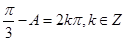 ,得
,得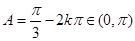 ,
所以
,
所以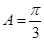 .
.
又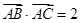 ,所以
,所以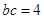 .
.
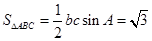 .
14分
.
14分
考点:1、三角函数的性质;2、向量的数量积;3、正弦定理.

练习册系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |