题目内容
已知函数f(x)=2cos ,在△ABC中,AB=1,f(C)=
,在△ABC中,AB=1,f(C)= +1,且△ABC的面积为
+1,且△ABC的面积为 .
.
(1)求角C的值;
(2)(理科)求sinA•sinB的值.
(文科)求△ABC的周长.
解:(1)由f(C)= +1得f(C)=2cos
+1得f(C)=2cos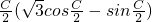 =
= +1
+1
sinC- cosC=-1 …2分
cosC=-1 …2分
sin(C- )=-
)=- …4分
…4分
所以C- =-
=- ,C=
,C= …6分
…6分
(2)(理科) S△ABC= =
=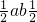 ?ab=2
?ab=2 …8分
…8分
设外接圆半径为R,则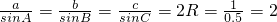 …11分
…11分
所以sinA•sinB=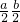 =
=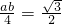 4分
4分
(文科)S△ABC= =
=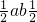 ?ab=2
?ab=2 …8分
…8分
c2=1=a2+b2-2abcos =a2+b2-6,所以a2+b2=7 …10分
=a2+b2-6,所以a2+b2=7 …10分
(a+b)2=a2+b2+2ab=7+4 所以a+b=2
所以a+b=2 …12分
…12分
所以周长 C△ABC=3+ .…14分.
.…14分.
分析:(1)利用已知条件f(C)= +1,函数f(x)=2cos
+1,函数f(x)=2cos ,通过两角差的正弦函数,求出C的三角函数,求出C的值.
,通过两角差的正弦函数,求出C的三角函数,求出C的值.
(2)理科利用三角形的面积以及正弦定理化简求解sinA•sinB的值.
文科:通过三角形的面积,余弦定理直接求出a+b的平方,利用周长求解即可.
点评:本题考查解三角形,正弦定理与余弦定理的应用,三角函数中的恒等变换应用,考查计算能力.
 +1得f(C)=2cos
+1得f(C)=2cos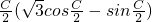 =
= +1
+1sinC-
 cosC=-1 …2分
cosC=-1 …2分sin(C-
 )=-
)=- …4分
…4分所以C-
 =-
=- ,C=
,C= …6分
…6分(2)(理科) S△ABC=
 =
=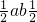 ?ab=2
?ab=2 …8分
…8分设外接圆半径为R,则
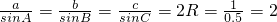 …11分
…11分所以sinA•sinB=
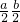 =
=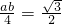 4分
4分(文科)S△ABC=
 =
=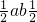 ?ab=2
?ab=2 …8分
…8分c2=1=a2+b2-2abcos
 =a2+b2-6,所以a2+b2=7 …10分
=a2+b2-6,所以a2+b2=7 …10分(a+b)2=a2+b2+2ab=7+4
 所以a+b=2
所以a+b=2 …12分
…12分所以周长 C△ABC=3+
 .…14分.
.…14分.分析:(1)利用已知条件f(C)=
 +1,函数f(x)=2cos
+1,函数f(x)=2cos ,通过两角差的正弦函数,求出C的三角函数,求出C的值.
,通过两角差的正弦函数,求出C的三角函数,求出C的值.(2)理科利用三角形的面积以及正弦定理化简求解sinA•sinB的值.
文科:通过三角形的面积,余弦定理直接求出a+b的平方,利用周长求解即可.
点评:本题考查解三角形,正弦定理与余弦定理的应用,三角函数中的恒等变换应用,考查计算能力.

练习册系列答案
相关题目