题目内容
若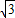
sinx-cosx=2m-3，则m的取值范围是 ．
【答案】分析：已知等式左边提取2变形后，利用两角和与差的正弦函数公式化为一个角的正弦函数，求出正弦函数的值域，列出关于m的不等式，求出不等式的解集即可得到m的范围．
解答：解：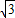
sinx-cosx=2（
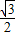sinx-
cosx）=2sin（x-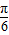
），
∵-1≤sin（x-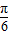
）≤1，
∴-2≤2sin（x-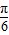
）≤2，
∴-2≤2m-3≤2，
解得：
≤m≤
，
则m的取值范围是[
，
]．
故答案为：[
，
]
点评：此题考查了两角和与差的正弦函数公式，以及正弦函数的定义域与值域，熟练掌握公式是解本题的关键．
解答：解：
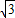sinx-cosx=2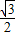（sinx-cosx）=2sin（x-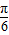），∵-1≤sin（x-
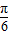）≤1，∴-2≤2sin（x-
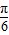）≤2，∴-2≤2m-3≤2，
解得：
≤m≤，则m的取值范围是[
，]．故答案为：[
，]点评：此题考查了两角和与差的正弦函数公式，以及正弦函数的定义域与值域，熟练掌握公式是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若sinx+cosx=1，那么sinnx+cosnx的值是（ ）
| A、1 | B、0 | C、-1 | D、不能确定 |
若sinx+cosx=
，x∈（0，π），则sinx-cosx的值为（ ）
| 1 |
| 3 |
A、±
| ||||
B、-
| ||||
C、
| ||||
D、
|