题目内容
已知函数 (a为常数,且a∈N*),对于定义域内的任意两个实数x1、x2,恒有|f(x1)-f(x2)|<1成立,则正整数a可以取的值有
(a为常数,且a∈N*),对于定义域内的任意两个实数x1、x2,恒有|f(x1)-f(x2)|<1成立,则正整数a可以取的值有
- A.4个
- B.5个
- C.6个
- D.7个
B
分析:由条件对定义域内任意x1,x2,满足|f(x1)-f(x2)|<1,问题可以转化为f(x)max-f(x)min<1,因此求函数的最值是关键.求最值时,利用换元法求解.
解答:由题意, ,
, ,
,
从而有 ,
, ,∴
,∴ 解得
解得  ,∵a∈N*,∴a=1,2,3,4,5,
,∵a∈N*,∴a=1,2,3,4,5,
故选B.
点评:解答时等价转化是解题的关键,求解函数的最值运用三角换元法,应注意参数角的范围.
分析:由条件对定义域内任意x1,x2,满足|f(x1)-f(x2)|<1,问题可以转化为f(x)max-f(x)min<1,因此求函数的最值是关键.求最值时,利用换元法求解.
解答:由题意,
 ,
, ,
,从而有
 ,
, ,∴
,∴ 解得
解得  ,∵a∈N*,∴a=1,2,3,4,5,
,∵a∈N*,∴a=1,2,3,4,5,故选B.
点评:解答时等价转化是解题的关键,求解函数的最值运用三角换元法,应注意参数角的范围.

练习册系列答案
相关题目
 ( a为常数、a∈R),
( a为常数、a∈R), .
. (a为常数)的图象经过点(1,3).
(a为常数)的图象经过点(1,3). ( a为常数、a∈R),
( a为常数、a∈R), .
. (a为常数)是R上的奇函数,函数
(a为常数)是R上的奇函数,函数
 上恒成立,求t的取值范围
上恒成立,求t的取值范围 其中a为常数,且
其中a为常数,且 .
.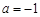 时,求
时,求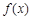 在
在 (e=2.718 28…)上的值域;
(e=2.718 28…)上的值域; 对任意
对任意 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.